Закон Ома в дифференциальной форме

Рис. 9.

Преобразуем закон Ома (3) к такой форме, которая была бы удобна для описания токов в произвольной среде. Для этого рассмотрим какую-либо трубку и применим закон Ома к малому ее участку длиной Dl (рис. 9):

,

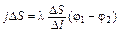где j – плотность тока на этом участке, а l – его удельная проводимость. Или, по сокращении на DS,

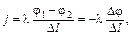
где Dj = 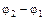– изменение потенциала в направлении j. Но скорость спадания потенциала 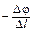вдоль какого-либо направления равна проекции вектора поля Е на это направление:

,

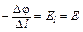ибо поперечных составляющих поля нет. Таким образом,

j = lE, (16)

где j, l и E – средние значения соответствующих величин внутри рассматриваемого объема трубки тока. Чем меньше этот объем, тем ближе они подходят к значениям в определенной точке проводящей среды. В пределе, при стягивании объема в точку, (16) переходит в локальное равенство, относящееся к этой точке. Если учесть, что величины j и Е суть векторы, причем, как следует из приведенных рассуждений, всегда одинаково направленные, то (16) можно записать в векторном виде, так что окончательно получим:

j = lE. (17)

Это равенство называется законом Ома в дифференциальной форме, хотя в него не входят производные, именно потому, что носит локальный характер, в противоположность интегральной форме (3) этого закона, связывающей величины, относящиеся к различным точкам проводящего пространства.

Из (17) следует, что в однородных средах (l = const) в областях, где ток течет под действием только электрических сил, линии тока совпадают с силовыми линиями электрического поля.