Условие стационарности токов

Самое общее условие стационарности, или постоянства, токов было сформулировано нами в начале этой лекции (условие (1)). Оно сводится к требованию, чтобы в любой точке проводящей среды объемная плотность заряда не менялась со временем. Поскольку любые изменения (или постоянство) этой плотности связаны с неизбежным движением электрических зарядов, условие это накладывает некие общие ограничения на распределение текущих по проводнику постоянных токов.

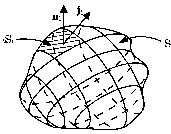Рис. 10.

Для выявления этих ограничений выделим внутри проводящей среды, несущей постоянный ток, произвольную замкнутую поверхность (рис. 10). Проходящий через эту поверхность полный ток (т. е. вытекающий изнутри) равен в соответствии с (9) потоку вектора jчерез нее. Но выходящий ток, по определению (2), есть «убыль» заряда, находящегося внутри S, в единицу времени, а из условия постоянства тока (1) этот заряд не может ни убывать, ни возрастать. Следовательно, общее условие стационарности токов может быть сформулировано следующим образом: поток вектора j через любую замкнутую поверхность равен нулю, т. е.

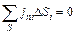, (18)

где суммирование производится по всем элементам поверхности S.

Следствие 1. Поскольку густота линий j пропорциональна j, то поток этого вектора через любую поверхность (как и для линий Е) пропорционален (алгебраическому) числу линий, пересекающих эту поверхность. Поэтому из условия (18) следует, что линии тока не имеют истоков, т. е. они не могут ни начинаться, ни кончаться (если бы такие точки существовали, то, окружая их замкнутыми поверхностями, мы получали бы отличный от нуля поток через них, ибо входило бы и выходило разное число линий, что противоречит (18)). Значит, они либо замкнуты, либо уходят в бесконечность двумя концами[10].

Понятно, что на практике реализуется всегда лишь первая возможность.

Следствие 2. Внутри однородных проводников, несущих постоянные токи, объемные заряды не образуются. Действительно, подставляя в (18) вытекающее из закона Ома (17) соотношение

j_n = lE_n

и вынося l = const за знак суммы, получим

.

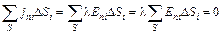Но по теореме Гаусса

,

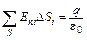где q – заряд внутри поверхности S. Стало быть, q = 0.

Полученный результат на первый взгляд может вызвать недоумение: то, что стационарность токов требует постоянства со временем объемной плотности зарядов в любой точке проводника – это понятно, но теперь мы доказали, что она (при l = const) должна быть равна нулю! Где же тогда располагаются заряды, создающие внутри проводника электрическое поле? Конечно же, они группируются не на зажимах источника, к которому подключен проводник: ведь внутри длинного однородного провода с током поле тоже однородно и заряды, расположенные на его концах, такое поле создать никак не могут (кулоновское поле убывает с расстоянием r от зарядов, как 1/ r2).

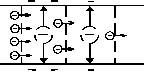Рис. 11.

Заряды, возбуждающие поле в проводнике с током, размещаются на его поверхности (разумеется, неравномерно). Процесс этот довольно сложен и происходит очень быстро (со скоростью, близкой к скорости света). При этом одна половина провода (подсоединенная к положительному выводу источника) заряжается положительно, другая – отрицательно. Для установления такого распределения зарядам не нужно смещаться на расстояния, сравнимые с длиной проводника: чтобы в какой-то ее области образовался избыточный, например, отрицательный заряд (рис. 11), нужно, чтобы с одной стороны в нее вошло больше «минусов», чем вышло с другой. При подключении провода к источнику заряды, скопившиеся, скажем, у его отрицательного полюса, «толкают» свободные одноименные носители близлежащего участка проводника, те «толкают» следующие и т. д. В итоге они лишь чуть-чуть смещаются (все по-разному), сообщая избыточный заряд каждому участку проводника, и затем (или одновременно) уходят на его поверхность, образуя необходимую поверхностную плотность для создания внутри однородного поля. Переходный процесс быстро заканчивается, и в дальнейшем устанавливается стационарное течение зарядов, образующих постоянный ток.

А если ток течет по проводнику сложной формы, в котором линии тока не параллельны? Может ли в произвольном случае необходимое поле быть образовано лишь поверхностными зарядами? Да, и мы в состоянии утверждать это не только на основании доказанного следствия 2. Чтобы поверхностным зарядам создать внутри проводника произвольное поле Е, нужно просто поместить его в это статическое поле (точнее, в противоположное ему). Тогда поверхностный заряд проводника «занулит» внутри это внешнее поле – Е, т. е. образует как раз требуемое поле Е.

Контрольные вопросы и задания

1. Существует ли внутри проводника с током электрическое поле? Является ли поверхность такого проводника эквипотенциальной?

2. Чем отличается поле постоянного тока, т. е. движущихся зарядов, от поля точно так же распределенных неподвижных зарядов?

3. Дать определение электрического тока. Это вектор или скаляр, алгебраическая (могущая быть отрицательной) или арифметическая (всегда положительная) величина?

4. Сформулировать закон Ома. Что называется напряжением, приложенным к концам проводника? Чем оно отличается от напряжённости электрического поля?

5. В каких единицах измеряются ток и сопротивление? Дать их определения.

6. Сформулировать первое начало термодинамики для проводника с постоянным током в установившемся режиме.

7. Сформулировать закон Джоуля.

8. Что называется плотностью тока? Это вектор или скаляр, алгебраическая или арифметическая величина?

9. Как связаны между собой ток, протекающий через какую-либо поверхность, и плотность тока в различных точках этой поверхности (могущая меняться от точки к точке)?

10. Что такое линия тока? Трубка тока?

11. Показать, что внутри однородного цилиндрического проводника ток равномерно распределён по сечению.

12. Показать, что сопротивление однородного цилиндрического проводника прямо пропорционально его длине и обратно пропорционально сечению проводника.

13. Описать методику расчёта сопротивления проводника произвольной формы.

14. Вывести формулы для расчёта сопротивления последовательного и параллельного соединений проводников.

15. Получить закон Ома в дифференциальной форме. Почему она называется дифференциальной?

16. Получить условие стационарности токов.

17. Показать, что линии тока не имеют истоков (точек обрыва).

18. Показать, что в однородных проводниках с постоянными токами не могут образовываться объёмные заряды. Почему это не выполняется для неоднородных проводников?

Лекция 15