Сопротивление однородного цилиндрического проводника

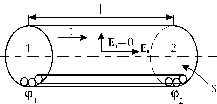Рис. 6

Каким же образом коэффициент пропорциональности в законе Ома – сопротивление проводника – зависит от его параметров? Попытаемся выделить в этой зависимости части, определяемые отдельно геометрией данного образца проводника и его материалом. Начнем с простейшего случая.

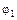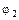Рассмотрим однородный цилиндрический проводник, по которому течет постоянный ток I (рис. 6). Пусть на перпендикулярных его оси сечениях 1 и 2, находящихся на расстоянии l друг от друга, поддерживаются потенциалы и . Какое поле будет при этом действовать внутри проводника? Как распределится ток по его сечению?

Ввиду однородности проводника и тождественности физических условий вдоль его оси любые перпендикулярные ей сечения абсолютно эквивалентны. Отсюда следует равенство нулю поперечной составляющей (ввиду аксиальной симметрии задачи она может быть только радиальной) поля 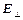, ибо если она существует в каком-то одном сечении, то она существует и во всех остальных. Эта составляющая повлечет за собой появление поперечного тока, который, дойдя до поверхности, должен оборваться, приводя к накапливанию у поверхности заряда и нарушая, таким образом, условие постоянства тока I[7]. Но если поле имеет лишь одну продольную составляющую, то оно обязано быть однородным не только по длине (что следует из эквивалентности сечений), но и по сечению (это вытекает из его потенциальности – см. § 8.14, пример 1). Таким образом, все линии тока оказываются параллельными оси, а трубки тока идентичны по сечению. Значит, вектор j постоянен по сечению проводника, а полный ток, текущий по нему,

I ~ S. (10)

Нетрудно видеть, что, кроме того,

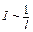. (11)

Действительно, «надставим» отрезок нашего проводника точно таким же куском с той же разностью потенциалов на концах. Получим проводник длиной 2l с током I и напряжением 2U = 2( 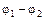). Уменьшим теперь напряжение на его концах до U. По закону Ома ток тоже уменьшится вдвое. Получаем, что при увеличении длины проводника в два раза и неизменном напряжении на его концах ток через него падает вдвое, т. е. зависимость (11).

Комбинируя (10) и (11), нетрудно видеть, что закон Ома может быть записан в следующем виде:

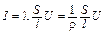, (12)

где l и r называются соответственно удельными проводимостью и сопротивлением проводника и являются константами, зависящими от свойств его материала[8]. Из сравнения (12) и (3) получаем формулу для расчета сопротивления однородного цилиндрического проводника

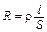. (13)

Отсюда может быть получена единица r в системе СИ – Ом×м; единица l, очевидно, есть обратная величина.