Сопротивление проводника произвольной формы

Рис. 7.

В случае проводника произвольной формы, сечения 1 и 2 которого находятся под напряжением U = 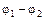(рис. 7), текущий по нему ток I (мы рассматриваем участок, не имеющий ответвлений) практически всегда может быть представлен в виде большого числа k достаточно тонких трубок тока.

Можно показать[9], что распределение токов в объеме проводника не изменится при варьировании напряжения между его концами. Другими словами, плотность тока j в каждой точке, оставаясь неизменной по направлению, по величине меняется пропорционально приложенному напряжению.

Таким образом, выделенные трубки тока при изменении напряжения не деформируются и можно применять закон Ома к каждой из них. Тогда для m-й трубки

,

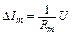где 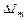– ток, текущий в m-й трубке, а 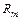– ее сопротивление. Складывая подобные выражения для всех k трубок, получим

,

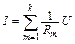откуда определится сопротивление R участка 1 – 2:

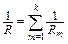. (14)

Разобьем далее каждую трубку тока на n участков, любой из которых с достаточной точностью можно считать цилиндрическим и однородным, и применим к ним формулу (13). Суммируя напряжения U_i на всех таких участках m-й трубки и приравнивая сумму полному напряжению U, действующему между ее концами, получим

,

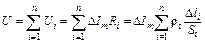где 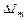– ток, текущий по m-й трубке, а 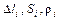– соответственно длина, сечение и удельное сопротивление i-го ее участка. Отсюда полное сопротивление рассматриваемой трубки тока

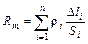(15)

(наше рассмотрение оказалось настолько общим, что допускает изменение проводимости среды от точки к точке).

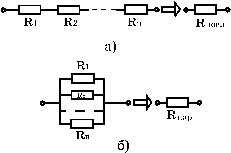Рис. 8

Итак, для расчета сопротивления проводника произвольной формы нужно разбить его на тонкие трубки тока, найти по (15) сопротивления каждой из них, а затем, используя (14), вычислить сопротивление всего участка проводника.

Замечание. Полученные формулы (15) и (14), очевидно, дают величины эквивалентных сопротивлений систем последовательно 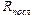и параллельно 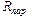соединенных проводников, изображенных на рис. 8 а и б:

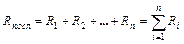, (15¢)

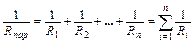. (14¢)

Следует отметить, что существуют более сложные схемы соединения сопротивлений, не сводящиеся к рассмотренным, на которых, однако, мы останавливаться не будем.