Закон Ома для участка цепи со сторонней ЭДС

Поскольку электрический ток – это движение зарядов под действием сил, а движение это определяется величиной и направлением этих сил, но не их природой, под совокупным действием электрического Е и стороннего 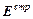полей возникнет, очевидно, ток, плотность которого по аналогии с (17л14)

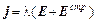. (2)

Это выражение представляет собой дифференциальную форму обобщенного закона Ома, из которой нетрудно получить и интегральную его форму. При этом мы ограничимся (достаточно общим) случаем так называемых квазилинейных трубок тока, или просто квазилинейных токов.

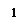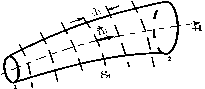Рис. 1

Под квазилинейной трубкой тока мы будем понимать такую трубку, для которой можно определить направление ее оси так, чтобы все электрические величины ( j, l, j, E, 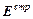и т. д.) в любом перпендикулярном этой оси сечении были постоянными в пределах заданной точности (но могли меняться от сечения к сечению) и чтобы вектор j плотности тока был параллелен (или антипараллелен) этой оси. Практически любой ток может быть представлен совокупностью достаточно тонких квазилинейных трубок. Введение понятия квазилинейного тока позволяет нам свести рассмотрение всего тока к рассмотрению его оси, которую мы будем называть контуром тока[11].

Итак, пусть дана квазилинейная трубка тока (рис.1). Выберем произвольно положительное направление ее оси + l и возьмем, идя вдоль него, два сечения 1 и 2. Разобьем полученный отрезок трубки перпендикулярными ее оси сечениями на n малых участков, причем направление положительной нормали n к каждому сечению выберем совпадающим с + l. Запишем обобщенный закон Ома (2) для i-го участка и умножим обе его части скалярно на элемент оси тока :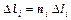

,

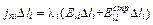где 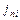, 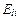и 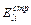– нормальные, или осевые, проекции соответствующих векторов. Просуммируем теперь полученные выражения вдоль всего отрезка оси трубки 1 – 2, разделив предварительно каждое из них на :

.

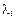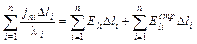Но 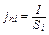, где I – ток внутри трубки, а 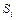– сечение i-го ее участка. Вынося I за знак суммы, получим

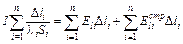. (3)

Нетрудно видеть, что

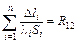
представляет собой не что иное, как сопротивление рассматриваемого отрезка 1 – 2 проводника (ср. (15л14)), а

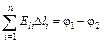
– разность потенциалов между первым 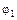и вторым 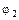его сечениями (если идти вдоль выбранного положительного направления его оси). Сумма же

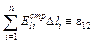(4)

называется сторонней электродвижущей силой, действующей на участке 1 – 2 проводника, и представляет собой работу сторонних сил по перенесению единичного положительного заряда от сечения 1 к сечению 2.

С учетом трех последних соотношений равенство (4) принимает следующий вид:

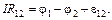(5)

Это выражение называется обобщенным законом Ома в интегральной форме. Оно показывает, что в случае действия сторонних сил произведение IR определяется алгебраической суммой электрического напряжения и сторонней ЭДС. Если на данном участке сторонние силы отсутствуют, 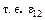= 0, то (5), естественно, переходит в закон Ома 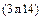в своей обычной (необобщенной) форме.