Законы Ома и Джоуля

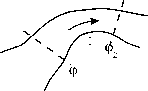Рис. 2.

Рассмотрим какой-либо участок протяженного проводника, ограниченный двумя его сечениями-эквипотенциалями (рис. 2), находящимися под разными потенциалами. Силой тока I, проходящего через заданное сечение проводника (или просто током), называется заряд, пересекающий это сечение в единицу времени:

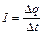, (2)

где Dq – заряд, перетекший за время Dt с одной стороны сечения на другую. Пока мы будем понимать под током положительную величину и вне зависимости от знака носителей считать его направленным в ту сторону, куда двигались бы положительные частицы, осуществляющие наблюдаемый перенос заряда. Другими словами, мы считаем ток текущим от большего потенциала к меньшему.

Основной закон постоянного тока – закон Ома, являющийся обобщением данных опыта, гласит: сила тока I, текущего по проводнику[4], пропорциональна разности потенциалов между его концами:

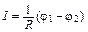, (3)

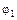где и 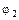– потенциалы первого и второго его сечения, если идти по направлению тока ( 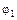> 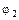), а коэффициент пропорциональности R, который и здесь принято писать в знаменателе, называется сопротивлением проводника. Коэффициент этот зависит от размеров и формы проводника, а также от его материала[5].

Единицей тока в системе СИ служит ампер:

1 А = 1 Кл/с,

а единицей сопротивления, которая определяется из закона Ома, – Ом:

1 Ом = 1 В/А,

т. е. 1 Ом – это сопротивление такого проводника, в котором возникает ток 1 А, если к его концам приложить разность потенциалов 1 В.

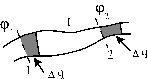Рис. 3.

Разность потенциалов 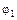– 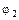между двумя произвольными точками поля, как это уже отмечалось, часто называют напряжением, действующим между этими точками, и обозначают буквой U. С учетом этого закон Ома (3) может быть записан также в виде

U = IR .

Обратимся теперь к энергетическим превращениям, происходящим внутри проводника, несущего постоянный ток. Пусть потенциалы концов какого-либо выделенного его участка равны 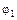и 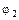(рис. 3) и за время Dt через сечение 1 внутрь этого участка вошел заряд Dq = IDt. Так как ток постоянный, то в соответствии с условием (1) суммарный заряд рассматриваемого отрезка проводника измениться не может и через другое его сечение 2 должен выйти такой же заряд Δq. Поскольку, кроме того, все электрические характеристики участка со временем не меняются, весь процесс сводится к переносу заряда Dq от сечения 1 с потенциалом 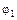к сечению 2 с потенциалом 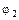. При этом электрические силы совершат, очевидно, работу

A¢ = Dq ( 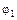– 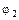) = U I Dt,

где 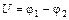– напряжение между сечениями 1 и 2. Если другие силы над рассматриваемым участком работы не совершают и его механическая энергия не меняется, т. е., как правило, если он неподвижен и в нем не происходит химических реакций, то по первому началу термодинамики

A¢ = DW + ,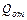

где DW – увеличение внутренней энергии проводника, приводящее к повышению его температуры T, а 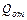– теплота, отданная окружающей среде. В установившемся режиме, когда T = const, DW = 0 и вся эта работа целиком выделяется в виде тепла. Это тепло называется джоулевым и может быть представлено с учетом закона Ома следующими выражениями:

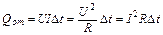, (4)

где R – сопротивление участка. Соотношения (4) представляют собой закон Джоуля для участка цепи.

Хотя в рамках нашего рассмотрения все эти выражения эквивалентны друг другу, область применимости последнего равенства оказывается гораздо шире областей применимости остальных. В следующей лекции мы увидим, что в случае действия на выбранном участке сил неэлектростатического происхождения эквивалентность этих соотношений нарушается и именно последнее из них определяет выделяющееся джоулево тепло. Поэтому мы сразу под джоулевым теплом 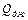будем понимать выражение

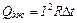, (5)

справедливое в самом общем случае действия внутри проводника сил любой природы.

Разделив (5) на Dt, мы получим так называемую мощность джоулевых потерь

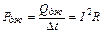, (6)

представляющую собой теплоту, выделяющуюся в единицу времени на данном участке с сопротивлением R при прохождении по нему тока I.

Прежде чем переходить к обсуждению введенной нами новой характеристики проводника – его сопротивления, рассмотрим еще несколько новых понятий.

Плотностью тока j называется заряд, протекающий в единицу времени через единицу перпендикулярного к направлению его движения сечения проводника. В общем случае произвольного проводника j может меняться от точки к точке, а потому по определению

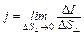, (7)

где 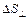– площадь перпендикулярной площадки, а DI – ток через нее. Мы наделим плотность тока свойствами вектора, т. е. помимо величины, даваемой (7), припишем ему определенное направление в пространстве. Это направление мы выберем совпадающим с направлением движения свободных носителей[6], если они положительны, и противоположно ему в случае отрицательного их знака. При таком определении j ток через малую произвольно ориентированную площадку DS (рис. 4)

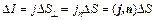, (8)

Рис. 4.

где 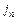– проекция вектора j на нормаль к площадке DS, а 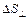– проекция площадки DS (на рис. не показана) на перпендикулярную к j плоскость. Тангенциальная составляющая 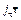вклада в ток не дает, ибо характеризует движение зарядов вдоль площадки DS, а не через нее.

Правая часть выражения (8) в зависимости от взаимной ориентации векторов j и n может принимать и отрицательные значения, и для того, чтобы оно было справедливым всегда, мы должны расширить данное нами ранее определение силы тока. В соответствии с этим, под силой тока, или током, через данную ориентированную поверхность мы будем понимать теперь алгебраическую скалярную величину, численно равную заряду, прошедшему через эту поверхность в направлении ее положительной нормали в единицу времени. Нетрудно видеть, что при таком определении ток через произвольную ориентирован­ную поверхность равен потоку вектора j через нее. Действительно, разбивая эту поверхность на малые площадки 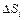и считая по формуле (8) ток 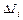через каждую из них, мы после суммирования этих выражений по всем элементам поверхности получим

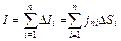, (9)

где левая часть этого равенства 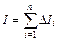представляет собой, очевидно, полный ток через поверхность, а правая – поток вектора j через нее.

Назовем линией тока направленную кривую, касательная к которой в каждой ее точке совпадает по направлению с вектором j. Очевидно, линия тока представляет собой траекторию движения бесконечно малого (но все же содержащего достаточное для усреднения число частиц) элемента заряда. Условимся проводить линии j с таким расчетом, чтобы их густота былапропорциональна величине j в данной области.

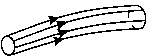Рис.5

Если через все точки какой-либо замкнутой кривой, лежащей внутри несущего ток проводника, провести линии тока, то мы получим так называемую трубку тока (рис.5), боковая поверхность которой состоит из этих линий. Понятно, что через боковую поверхность трубки тока заряд не переносится (ибо на этой поверхности 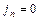), а потому ток через любое ее сечение оказывается одним и тем же.