Теорема (О башне полей).

Если имеется цепочка конечных расширений полей P > L > K, то степень итогового расширения равно произведению степеней промежуточных расширений .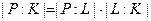

Доказательство.

Если базисные элементы векторного пространства P над L умножить поэлементно на базисные элементы пространства L над K, то получится требуемый базис. Это нужно проверить или самому или посмотреть в любой книжке по теории полей.

Теорема (вторая теорема о полях Галуа).

Каждое конечное поле содержит в качестве подполя некоторое поле вычетов GF(p) и поэтому имеет порядок вида pⁿ , для подходящего натурального числа n.

(Таким образом, ответ на один из вопросов получен – число элементов в конечном поле всегда является степенью простого числа. Уже теперь можно утверждать, что полей порядка 6 или 82 не существует.)

Доказательство.

а)Пусть Р – конечное поле и e – его нейтральный элемент по умножению. Рассмотрим суммы нейтрального элемента самого с собой: e, e+e, e+e+e, … Т.к. поле конечное, то суммы начнут повторяться, например, ne=me, n<m. Вычитая их друг из друга получаем, что (m—n)e=0. Покажем, что на самом деле число m–n является простым (оно называется характеристикой поля). Если бы это число было составным, то мы, по определению нейтрального элемента по умножению, получили бы 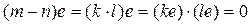. Т.к. в поле нет делителей нуля, то или ke=0 или le=0. Если опять k или l - составное число, повторяем процедуру вновь.

б) Итак, для некоторого простого числа p, в поле P содержится полугруппа по сложению, состоящая из элементов {e, 2e, 3e, …, (p-1)e, 0}. Остается проверить, что эта полугруппа изоморфна полю вычетов Z_p={1,2,3,…,p-1,0}. Как задается изоморфизм совершенно очевидно, элемент ke переходит в элемент k. Проверка свойств изоморфизма стандартна.

в) Пусть P, как векторное пространство над Z_p, имеет размерность n. Пусть b₁, b₂, …, b_n – базис. Тогда каждый элемент из P может быть записан в виде 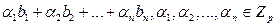. А таких записей ровно pⁿ штук. Теорема доказана.

□

Характеристика, упомянутая нами вскользь выше у полей обязательно является простым числом. Но кольца могут иметь характеристику, равную любому натуральному числу.

Определение. Наименьшее натуральное число n, такое, что для любого элемента a кольца К выполняется условие na=a+a+…+a=0 называется характеристикой кольца.

Например, характеристики колец Z₁₄, Z₈[x], M₅(Z₁₂₅) равны 14, 8 и 125 соответственно.

Если поле имеет характеристику p, т.е. сумма любых p элементов равна 0, то в нем верна формула (a+b)^p=a^p+b^p. Дело в том, что по формуле бинома Ньютона все промежуточные биномиальные коэффициенты будут кратны p и, поэтому, все промежуточные слагаемые обнулятся. Эта формула имеет очевидное обобщение .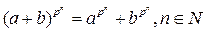

Наша главная цель показать, что для любой степени pⁿ существует поле Галуа данного порядка. Но для этого придется ввести еще одно важное понятие.

Определение. Пусть f(x) - многочлен над полем P. Поле L>P называется полем разложения многочлена f(x), если все корни многочлена f(x) принадлежат полю L, и оно порождается этими корнями. Т.е. это минимальное поле, содержащее все корни многочлена f(x).