Теорема (Основная теорем о евклидовых кольцах).

Пусть К – евклидово кольцо, тогда любые элементы имеют наибольший общий делитель и, более того, 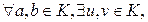такие, что d=НОД(a,b)=au +bv.

Доказательство.

а) Применяя свойство деления с остатком получим табличку уменьшающихся остатков. Так как степень каждого остатка – натуральное число, а натуральные числа не могут убывать бесконечно, то табличка будет конечной, а последний остаток нулевым.

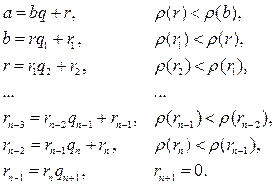
В нашей табличке получилось n+2 строки. Какой же из участвующих в ней элементов является долгожданным НОД? Это последний ненулевой остаток r_n. Для того, чтобы убедиться, что d=r_n, нужно проверить оба свойства НОД. Прежде всего, просматривая табличку снизу вверх, убеждаемся, что r_n делит a и b. В самом деле, последняя строка нам гарантирует, что r_n\r_n-1. Из предпоследней строки следует, что r_n\r_n-2 и т.д. Из третьей строки следует, что r_n\r, из второй, что делит b, а из первой, что r_n\a.

Теперь проверим, что r_n - наибольший делитель, т.е., что он делится на любой s такой, что s\a и s\b. Теперь просматриваем нашу табличку сверху вниз. Из первой строчки следует, что s\r, из второй, что s\r₁ и т.д. Из предпоследней строки следует, что s\r_n. Таким образом, последняя строка даже не понадобилась.

б) Осталось выразить остаток r_n через исходные элементы a и b. Для этого опять просматриваем нашу табличку снизу вверх. Из предпоследней строки получаем r_n =r_n-2+(-q_n)r_n-1, из третьей снизу r_n-1=r_n-3+(-q_n-1)r_n-2, поэтому

r_n=r_n-2+(-q_n)r_n-1=r_n-2+(-q_n)(r_n-3+(-q_n-1)r_n-2)=r_n-2(1+(-q_n)(-q_n-1))+r_n-3(-q_n).

Поднимаясь снизу вверх, мы последовательно выразим r_n через r_n-2 и r_n-1, потом через r_n-3 и r_n-2 и т.д. И, наконец, через a и b.

□

Таким образом, в кольце целых чисел и кольце многочленов над полем всегда можно эффективно найти НОД. Алгоритм, приведенный выше, его называют алгоритмом Евклида, реализован в большинстве компьютерных систем, в том числе и в тех, что используются для нужд криптографии.

Данная теорема имеет массу приложений, например, с ее помощью строятся поля Галуа.