Теорема (О поле разложения).

Для любого поля P и любого многочлена 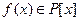существует поле разложения. С точностью до изоморфизма это поле единственно.

Доказательство

идейно совпадает с доказательством с первой теоремы о полях Галуа. Только простой элемент кольца целых чисел заменяется на простой элемент кольца многочленов. Поскольку оба кольца евклидовы, то рассуждения идентичны.

а) Поскольку каждый многочлен однозначно раскладывается в произведение неприводимых многочленов, то можем сразу считать, что многочлен f(x) неприводим.

б) После этого вместо остатков от деления на простое число p рассматриваем все остатки от деления на многочлен f(x). Как и в кольце вычетов вводим операции сложения и умножения. Т.е. в качестве результата берем не обычную сумму и произведение, а остаток от деления на многочлен f(x). Как и в случае колец вычетов проверяется, что получается коммутативное кольцо с единицей.

в) Проверим, что любой ненулевой остаток g(x) имеет обратный по умножению. Т.к. степень многочлена g(x) меньше, чем степень многочлена f(x), а он, в свою очередь, неприводим, то НОД(f(x),g(x))=1. Теперь по алгоритму Евклида в кольце P[x] найдутся многочлены u(x), v(x), такие, что u(x)g(x)+v(x)f(x)=1. Отсюда заключаем, что обратным к остатку g(x) является остаток от многочлена u(x).

г) Теперь можно указать элемент, который в построенном поле остатков, обозначим его L, будет корнем многочлена f(x). Конечно – это остаток, равный многочлену “x”.

д) Теперь в поле L разлагаем многочлен f(x) на неприводимые множители, а хотя бы два множителя появится, ведь один корень уже появился, и возвращаемся к началу доказательства.

е) Вопрос о единственности кажется очевидным – просто добавили корни, а они-то только от многочлена зависят, и получили единственное поле. Однако вопрос гораздо тоньше, но мы его обсуждать не будем.

□

Поскольку доказательство теоремы несколько описательное и поясняет только идеи (поскольку это не учебник по алгебре), а не детали, то разумно рассмотреть пример.

Пример 1. В современном алгоритме шифрования AES, пришедшем в 26.11.2001 на смену DES, используется конечное поле Галуа GF(2⁸). Это поле является расширением самого маленького поля GF(2), которое состоит из двух нейтральных элементов {0,1}. Неприводимый многочлен, с помощью которого оно строится, согласно стандарта США FIPS-197, имеет вид

f(x)=x⁸+x⁴+x³+x+1. Неплохое упражнение вручную проверить, что многочлен неприводим. Пусть g(x)=x⁷+x³+x+1. Этот остаток задает, согласно FIPS-197, байт со следующими битами 10001011. Одно из основных криптографических преобразований алгоритма AES состоит в том, что элемент поля g(x) преобразуется в обратный к нему по умножению g^-1(x).

Воспользуемся алгоритмом Евклида. Нужно найти такие остатки u, v, что ug+vf=1. Составляем табличку деления с остатком

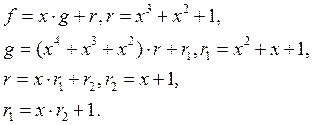
Теперь нужно выразить последний остаток, равный 1, последовательно через все предыдущие остатки, а потом и через f и g. Обратим внимание, что мы работаем в поле характеристики 2, поэтому x=-x, и (a+b)²=a²+b²:

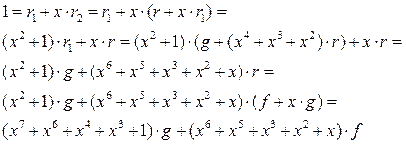
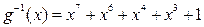Итак, получилось, , т.е. и, значит, байт 10001011 под действие одного шага алгоритма AES перейдет в байт 11011001.

Потренируйтесь проверяя наш ответ, перемножьте многочлены g и u, а потом найдите остаток от деления на многочлен f. Остаток должен получиться равным 1.