Теорема (Третья теорема о поле Галуа).

Для любого простого числа p и натурального числа n существует единственное поле Галуа GF(pⁿ), которое является полем разложения многочлена .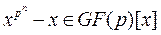

Доказательство.

По теореме о поле разложения, поле разложения нашего многочлена существует и оно единственно. Нужно только проверить, что оно содержит pⁿ элементов. Поскольку наш многочлен имеет степень pⁿ, то получается, что поле разложения должно состоять исключительно из корней самого многочлена!

Вначале проверим, что разных корней ровно pⁿ штук. Т. к. у многочлена над полем не может быть корней больше, чем его степень, то нужно выяснить есть ли кратные корни. Если бы они были, то многочлен и его производная имели бы общие делители. Однако производная многочлена равна 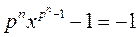(потому, что характеристика поля равна p).

Теперь проверим, что корни образуют в поле разложения подполе, а, значит, совпадают с полем разложения, ведь оно минимальное поле, содержащее все корни.

Пусть a и b – корни нашего многочлена. Нужно проверить, что тогда a+b, ab, -a, a^-1, а также 0 и 1, тоже являются корнями многочлена. Для 0 и 1 это очевидно. Далее, по предположению имеем 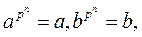поэтому, не забывая, что характеристика равна p, получаем

□

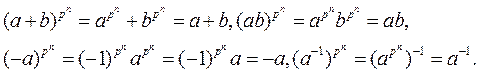
Вычисления, выполненные нами при нахождении обратного элемента по умножению, оказались довольно громоздкими. Конечно, на компьютере они будут выполнены мгновенно. Однако, если степень многочлена будет в несколько сотен единиц, и решать придется много уравнений, компьютеру тоже мало не покажется. Кроме того, в машинном виде идеально любые объекты представлять в виде чисел и все сводить к операциям над числами. Но чтобы связать числа с элементами конечного поля нам нужно ввести одно важное понятие.

Определение. Порождающий элемент мультипликативной группы поля, если он существует, называется примитивным элементом.