Оценка значимости коэффициентов модели.

Для упрощения полученной модели проверяют значимость ее коэффициентов. Ее выполняют для каждого коэффициента отдельно. Оценка значимости коэффициентов производится по критерию Стьюдента, либо по доверительному интервалу, который при использовании факторного эксперимента одинаков для всех коэффициентов.

Критерий Стьюдента

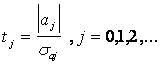, (6.39)

где 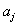— j-й коэффициент уравнения регрессии;

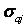— среднее квадратичное отклонение коэффициента .

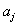Диагональные элементы ковариационной матрицы 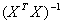равны между собой, поэтому все коэффициенты уравнения регрессии определяются с одинаковой точностью:

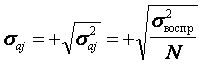, (6.40)

где 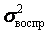— дисперсия воспроизводимости.

Дисперсия воспроизводимости, как правило, определяется с помощью повторных опытов в нулевой точке (центре эксперимента):

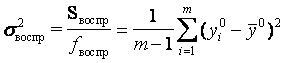, (6.41)

где 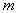— число повторных опытов;

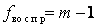— число степеней свободы дисперсии воспроизводимости;

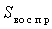— остаточная сумма квадратов воспроизводимости;

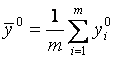. (6.42)

Таким образом, вычисляют 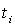для каждого i-го коэффициента. Для 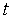-критерия имеются специальные таблицы распределения Стьюдента, рассчитанные для различных 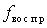, 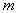и доверительных вероятностей 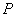(уровней значимости ).

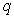Коэффициент 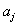считается значимым (значимо отличается от нуля) с некоторой доверительной вероятностью, если вычисленный 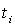больше табличного значения 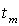при такой же доверительной вероятности и соответствующем числе степеней свободы.

Для оценки значимости коэффициентов по доверительному интервалу вычисляют доверительный интервал для j-го коэффициента по формуле

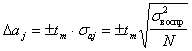. (6.43)

Как было отмечено выше, доверительный интервал 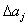одинаков для всех коэффициентов. Определение значимости коэффициентов уравнения регрессии с помощью соотношения (6.43) удобно тем, что позволяет применить правило: коэффициент значим, если его абсолютная величина больше доверительного интервала.

Незначимые коэффициенты исключаются из модели. При этом если коэффициенты модели некоррелированны между собой (матрица моментов диагональная), то исключение незначимых коэффициентов не скажется на остальных коэффициентах. В обратном случае оставшиеся коэффициенты пересчитываются заново, поскольку коэффициенты закоррелированы друг с другом.