Анализ особенностей МГУА.

1. На начальных стадиях аппроксимации экспериментальных данных 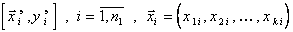отношение числа 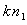этих данных к числу коэффициентов частных полиномов, определяемых в совокупности, намного больше единицы. Вследствие этого коэффициенты “наилучших” полиномов, приближающих точки 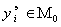и, отчасти, 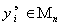, весьма слабо зависят от помехи, налагаемой на выходную координату объекта, а СКО ММ остается примерно одинаковой как на 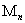, так и на 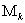. 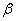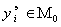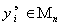С увеличением номера стадии возрастает число аргументов полинома и общее число коэффициентов, определяемых по точкам и , что, естественно, приводит к уменьшению величины 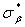. Одновременно с ростом 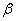уменьшается отношение числа экспериментальных данных к числу определяемых коэффициентов (это отношение может стать <1 ). Поэтому получаемая ММ фактически интерполирует 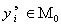и, отчасти, 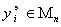, т.е. весьма точно описывает неточные экспериментальные данные, искаженные случайными помехами . ММ, коэффициенты которой найдены интерполиационным методом по случайным величинам, не может надежно описывать независимые экспериментальные данные 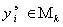, поэтому во многих случаях величина 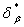будет нарастать с увеличением номера стадии .

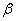Такое явление будем называть неустойчивостью МГУА.

Неустойчивость МГУА наблюдается и при анализе величины 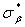, которая часто убывает с ростом 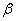, а затем начинает также возрастать. Величина 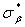менее чувствительна к росту 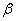, так как данные 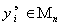участвуют в формировании ММ.

Для предотвращения неустойчивости МГУА в работах Ивахенко А.Г. рекомендуется выбрать число стадий 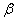из условия минимума 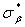. Но во многих случаях величина 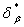более чувствительна к увеличению 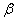и более целесообразно оканчивать процесс аппроксимации, как только 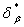достигнет своего минимума.

2. После завершения процесса аппроксимации строится окончательное выражение функции 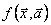путем последовательного исключения промежуточных аргументов. При большом числе стадий структура модели 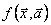может оказаться весьма сложной и неудобной в расчетах. В таких случаях 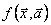задается набором полиномов.

3. Остановимся теперь на правиле отбора “наилучших” полиномов. По существу в МГУА отсутствует формализованная процедура выбора на каждой стадии таких полиномов, на базе которых можно построить функцию 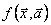, описывающую экспериментальные данные 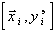с заранее заданной погрешностью. Можно только предполагать, что подобные полиномы находятся среди тех частных полиномов, СКО аппроксимации которых точек 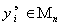относительно малы. Чрезмерное уменьшение (особенно на начальных стадиях) числа отбираемых полиномов увеличивает вероятность потери настоящих аргументов функции 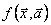; чрезмерное увеличение ведет к резкому росту объема вычислений. Поэтому на каждой стадии целесообразно отбирать примерно одно и тоже число 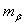полиномов с наименьшими значениями 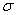. Если при выбранном наугад числе 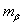не удается построить желаемую функцию 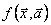, то все расчеты повторяются при другом, несколько большем .

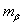4. В методе МГУА не требуется предварительно задавать структуру модели 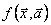. Она формируется в процессе многостадийного отбора “наилучших” частных полиномов.

5. Полученная данным методом зависимость 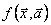может быть функцией меньшего чем 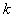числа входных переменных 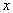. При исследовании сложных объектов всегда имеется опасность включения в число входных координат таких факторов, влияние на 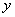которых незначимо или не может быть оценено при данном уровне помех. Устранение из ММ таких незначимых факторов также осуществляется МГУА в процессе многостадийного отбора “наилучших” частных моделей.

6. Число стадий аппроксимации зависит от многочисленных факторов. Важнейшими из них являются число входных координат, допустимая погрешность ММ, структура частных полиномов, число отбираемых полиномов, соотношение чисел 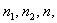уровень помехи и др.

7. При использовании МГУА на каждой стадии имеем дело с матрицей системы нормальных уравнений МНК порядка, не превышающего 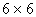, что, в общем случае, способствует улучшению ее обусловленности. Если же размерность вектора частных полиномов равна 3-4, то появляется возможность сравнительно просто оценивать степень обусловленности матрицы 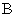системы нормальных уравнений МНК по критерию Фоке

,

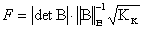где 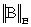— эвклидова норма матрицы В с элементами ;

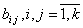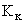— порядок матрицы ;

.

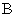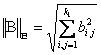Частные полиномы, матрицы 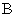которых плохо обусловлены, т.е. величины 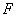малы, не должны включаться в число отбираемых на следующую стадию.

В настоящее время многие вопросы применения и обоснования МГУА еще нуждается в детальной разработке, недостаточен и опыт его применения для решения задач моделирования объектов.

Практическая рекомендация по группировке исходных данных 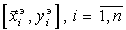по множествам 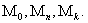Определяются среднее арифметическое значение 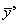по всем данным и отклонения случайных величин 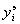от 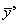. Ординаты 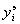, обладающие наибольшими отклонениями включают в 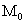, наименьшими — в 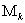, остальные — в .

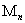Структура алгоритма самоорганизации модели на ЭВМ.Многорядный алгоритм селекции с пороговым самоотбором реализует МГУА. Его можно эффективно применять для большого числа переменных (до 1000), когда таблица исходных экспериментальных данных содержит всего 15-20 точек.

Структурная схема алгоритма показана на рис.3.5

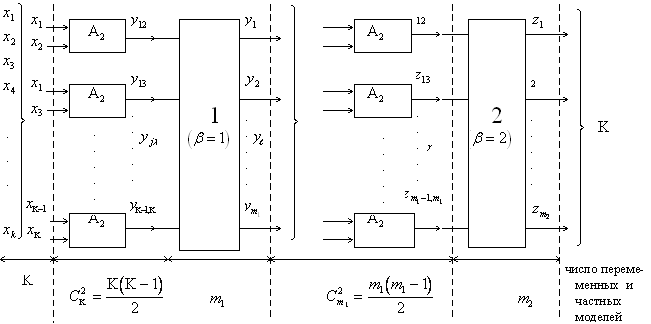
Рис.3.5

Здесь: 1,2 — пороговые отборы 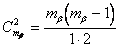лучших частных моделе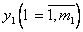й и 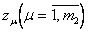по критерию селекции;

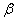— номер ряда селекции;

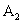— алгоритм попарной обработки переменных.

В первом ряду селекции образуются всевозможные пары аргументов, и для каждой из них находится частная модель вида

,

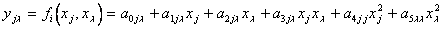где ;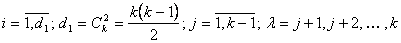

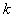— число входных переменных первого ряда селекции.

Оценки коэффициентов частных моделей 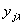рассчитываются МНК по части опытных данных, называемой обучающей последовательностью. Из всех частных моделей выбирается 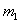лучших моделей .

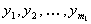Во втором ряду селекции образуются пары выходных переменных, прошедших первый ряд и для каждой из них находятся частные модели второго ряда 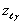и т.д.

Число предложенных алгоритмов МГУА непрерывно возрастает, но все они основаны на указанном выше едином принципе самоорганизации.