Определение наилучшей модели

Критерий выбора модели. При анализе сложных систем большое практическое значение имеют способы определения наилучшей модели объекта из некоторой их совокупности. Рассмотрим этот вопрос на примере регрессионных моделей.

Цель предварительного выбора наилучшей модели достигается применением в отдельности или в некоторой совокупности следующих критериев:

 наименьшее число коэффициентов модели, совместимое с заданной допустимой погрешностью;

 простота структуры модели, совместимая с допустимой погрешностью;

 разумные физические основания;

 минимальная сумма квадратов отклонений между предсказанными 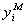и эмпирическими значениями 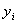выходной переменной y;

 минимальная оценка дисперсии 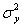выходной переменной.

Анализ погрешностей. Прежде всего, при оценке моделей проводят анализ остатков (погрешностей) в виде разностей 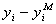. В регрессионном анализе используется ряд основных предположений:

 независимость ошибок;

 постоянства их дисперсий;

 нормальный закон распределения ошибок.

Если модель адекватно описывает экспериментальные данные, то погрешности должны не противоречить этим предположениям. Анализ погрешностей - это способ проверки того, что то или иное предположение не нарушено.

Можно выделить следующие наиболее характерные результаты анализа погрешностей:

1. Обнаружение выбросов, т.е. резко отличающихся, экстремальных значений 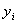от предполагаемого значения 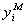. В этом случае необходимо повторить эксперимент в точке выброса, предварительно проверив правильность его условий. Если выброс устойчив, то его надо или выбросить и пересчитать коэффициенты модели без него, или исследовать физическую природу его существования.

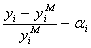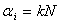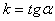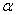2. Обнаружение некоторого тренда в остатках, т.е. тенденции в их изменении с течением времени. Например, в остатках наблюдается тенденция к линейному росту. Для улучшения модели вычисляют поправку в виде разности , где , , - угол наклона усредненной линии остатков к оси абсцисс, N - номер эксперимента.

3. Обнаружение разного сдвига уровня процесса. В этом случае нужно выяснить причину резкого скачка погрешности, а затем разбить выборку на две и для каждого уровня построить модель.

4. Обнаружение изменений в дисперсии ошибки. Анализ, который проводят при построении регрессионных моделей, позволяет найти некоторое среднее значение дисперсии ошибки (например, дисперсию воспроизводимости). Если дисперсии ошибки неоднородны, то найденная средняя дисперсия может неверно описывать часть экспериментальных данных.

5. Исследование остатков для проверки того, описываются ли они нормальным законом распределения. В этом случае можно проверить случайность значений остатков и воспользоваться кривой нормального распределения.

Сравнение двух регрессионных моделей. Рассмотрим некоторые методы сравнения регрессионных моделей, применимые как к линейным, так и нелинейным моделям.

1. Критерий Хоэла. Предполагается, что имеется адекватная модель 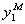, которая удовлетворительно описывает экспериментальные данные в области ее применимости. С ней конкурирует другая модель 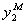. Ставится задача: не следует ли отказаться от модели 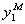и отдать предпочтение модели 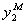. Строят тестовую линейную зависимость в виде уравнения в параметрической форме

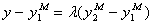, (6.69)

где >0. Проверка сводится к оценке в уравнении (6.69) углового коэффициента (параметра) . Если  значимо положителен (1), от модели 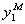отказываются в пользу второй модели 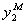. Действительно, из (6.69) имеем:

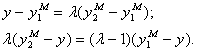
Обозначим 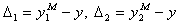- ошибки модел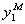и и .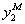

Тогда .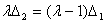

Отсюда при 1 имеем

.

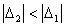Если  незначимо положителен (<1), то нельзя определить, какая из моделей лучше. Действительно, <1 не дает определенного результата, так как возможно выполнение и неравенства 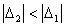(в пользу модели 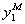) и противоположного ему неравенства 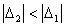(в пользу модели 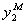), т.е. неизвестно условие нарушения неравенств. В этом случае отдается предпочтение модели .

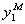Критерий Хоэла называется несимметричным, так как он может использоваться только при >0. Таким образом, подставляя в уравнение (3.69) значения 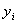, , 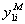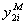можно дать оценку погрешностей регрессионных моделей 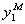, 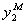и выбрать путем оценки параметра  лучшую из них.

2. Критерий Вильяма и Клута. Для сравнения двух регрессионных моделей, которые, по крайней мере, первоначально представляются равноценными, можно использовать симметричный критерий Вильяма и Клута. Проверка осуществляется путем оценки параметра  в тестовом уравнении

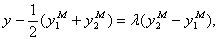(6.70)

где y принимает эмпирические значения. Предположим, что модель 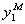удовлетворительна тогда

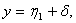( 6.71)

где ₁- теоретическое значение, предсказанное первой моделью в предположении, что ее коэффициенты регрессии вычислены точно,  - погрешность модели. Подставляя (6.71) в (6.70) получим

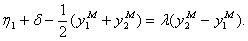(6.72)

Вследствие того, что модель 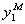достаточно адекватна, можно положить 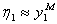и преобразовать выражение (6.72) к виду

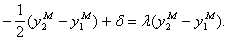
Отсюда при малых ошибках  следует, что модели 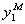отдается предпочтение при .

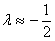Теперь предположим, что удовлетворительна модель 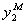, тогда

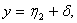(3.73)

Подставляя (3.73) в (3.71) и предполагая, что 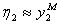, получим

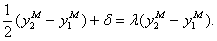
Следовательно, если верна модель 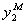, то получим оценку .

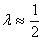Таким образом, значимое отрицательное значение параметра 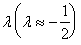указывает на то, что модель 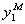лучше модели 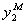. Если  значимо положителен, то окажется лучше модель 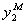. Если  незначительно отличается от нуля, то выбора между двумя моделями сделать нельзя - они равнозначны.

Итак, подставляя в уравнение (6.70) значения 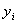, , 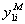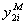взятые из допустимой области применения регрессионных моделей 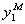, 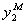можно путем количественной оценки параметра  выбрать лучшую из этих моделей. критерий Вильяма и Клута называется симметричным, так как он может применяться и при положительных и при отрицательных значениях .

Приложение 1

Основные технические характеристики логического анализатора В-141:

Каналы:

· Число входных измерительных каналов – 32

· Активные 8-канальные пробники (4 пробника)

· Параметры входов – 100 МОм, 10 пФ

· Полоса пропускания входного тракта – 0 …200 Мгц

· Входной диапазон анализируемых сигналов - ±5 В

· Программная установка уровня дискриминации анализируемых сигналов в пределах всего входного диапазона с дискретностью 150 мВ

Общие:

· Максимальная частота дискретизации сигнала – 400 МГц

· Максимальная глубина памяти – 128 квыб

· Внутреннее (от встроенного генератора) и внешнее (от сигнала любого из входных каналов) тактирование

· Генерация сигналов ТТЛ по 16 каналам с максимальной частотой дискретизации сигнала 100 МГц

Основные рабочие конфигурации анализатора:

· Анализ сигналов от произвольных 8 входных каналов с частотой дискретизации сигнала до 400 МГц и глубиной памяти до 128 Квыб/канал

· Анализ сигналов от произвольных 16 входных каналов с частотой дискретизации сигнала до 200 МГЦ и глубиной памяти до 64 Квыб/канал

· Анализ сигналов от каждого из 32 входных сигналов с глубиной памяти до 32 Квыб/канал и частотой дискретизации сигнала в диапазоне от 1 МГц до 100 МГц

Режимы запуска развертки:

· От произвольного входного каналу о заданному перепаду логических уровней

· По заданной комбинации логических уровней от 2 до 32 произвольных входных каналов

· От произвольного входного канала по заданной последовательности логических уровней, а также с учетом их длительности

· По заданной последовательности комбинаций логических уровней от 1 до 32 произвольных каналов с учетом их длительности

Прочие:

· Аппаратно-логический анализатор/генератор цифровых сигналов В-141 включает в себя корпус УНИПРО с блоком питания и интерфейсом В-101 и измерительный модуль В-141

· Интерфейсы с компьютером:

o Принтерный порт, протоколы ECP/EPP;

o Последовательный порт RS-232

· Питание 220 В/50 Гц

· Потребление 15 Вт

· Размеры:

o Измерительного модуля В-141-190x140x120 мм;

o Комплекса УНИПРО – 290x260x70мм.

· Масса:

o Измерительного модуля В-141-0,8 кг

o Анализатора/генератора В-141 в сборе – 2,3 кг.