Метод группового учета аргументов
При построении математических моделей сложных объектов необходимо учитывать следующие их особенности:
высокая размерность вектора входных координат 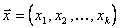 ;
;
наличие большого числа внутренних источников случайных помех, статистические характеристики которых, как правило, неизвестны;
неизученность механизмов действия различных экономических, социальных и физико-химических явлений и процессов в объектах;
трудность постановки экспериментов для получения большого числа сигналов 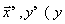 — одномерный выход объекта ).
— одномерный выход объекта ).
Указанные особенности затрудняют построение неформальных ММ сложных объектов и вынуждают описывать статические режимы их функционирования уравнениями вида
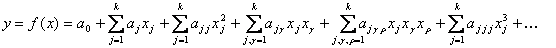 (6.62)
(6.62)
где 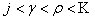 ;
;
 — вектор неизвестных коэффициентов размерности
— вектор неизвестных коэффициентов размерности 
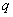 ;
;
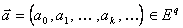 .
.
Если порядок 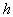 полинома по всем переменным
полинома по всем переменным 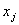 равен числу
равен числу 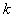 входных координат
входных координат 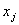 , то выражение (3.62) называют полным полиномом Колмогорова-Габбора.
, то выражение (3.62) называют полным полиномом Колмогорова-Габбора.
При увеличении числа входных координат 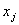 размерность вектора
размерность вектора  полного полинома возрастает исключительно быстро. Так, например, при
полного полинома возрастает исключительно быстро. Так, например, при 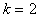 размерность вектора
размерность вектора  равна 6, при
равна 6, при 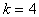 она возрастает до 70.
она возрастает до 70.
Для определения вектора  математической модели сложного объекта по экспериментальным данным
математической модели сложного объекта по экспериментальным данным 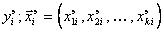 при
при 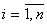 часто применяют МНК.
часто применяют МНК.
При этом сталкиваются с двумя затруднениями:
1. Вследствие слабой изученности сложных объектов многие входные координаты, включенные в ММ, оказываются сильно коррелированными, что приводит к плохой обусловленности системы нормальных уравнений МНК. Высокая размерность вектора  делает невозможным какой-либо предварительный анализ степени обусловленности матрицы системы уравнений. Поэтому исследователь вынужден убеждаться в неустойчивости задачи определения
делает невозможным какой-либо предварительный анализ степени обусловленности матрицы системы уравнений. Поэтому исследователь вынужден убеждаться в неустойчивости задачи определения  лишь в результате ее многократного решения на ЭВМ.
лишь в результате ее многократного решения на ЭВМ.
2. Задача определения вектора  заранее не заданной размерности
заранее не заданной размерности 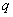 полинома типа (6.62) является, как правило, неустойчивой. Обоснованный же выбор числа
полинома типа (6.62) является, как правило, неустойчивой. Обоснованный же выбор числа 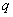 структуры полинома (6.62) фактически невозможен из-за большой размерности таблицы экспериментальных данных:
структуры полинома (6.62) фактически невозможен из-за большой размерности таблицы экспериментальных данных:
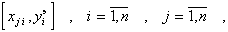
и высокого уровня помех, налагаемых на выходную координату объекта. Вследствие этого при построении ММ размерность вектора  и структура полинома (6.62) задаются в какой-то мере наугад; затем с помощью МНК определяются значения
и структура полинома (6.62) задаются в какой-то мере наугад; затем с помощью МНК определяются значения 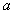 ; вычисляется СКО
; вычисляется СКО 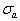 аппроксимации полиномом (6.62) тех табличных данных
аппроксимации полиномом (6.62) тех табличных данных 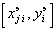 , которые не были использованы для нахождения
, которые не были использованы для нахождения  ; величина
; величина 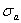 сравнивается с допустимой ошибкой
сравнивается с допустимой ошибкой  ММ. Если
ММ. Если 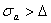 , размерность
, размерность  увеличивают и (или) видоизменяют структуру ММ (6.62), определяют новые значения
увеличивают и (или) видоизменяют структуру ММ (6.62), определяют новые значения 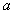 (напомним, что ряд (6.62) не является ортогональным). Затем снова вычисляют величину
(напомним, что ряд (6.62) не является ортогональным). Затем снова вычисляют величину 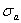 , сравнивают ее с
, сравнивают ее с  и повторяют описанную процедуру до тех пор, пока при некоторой структуре полинома (6.62) и размерности
и повторяют описанную процедуру до тех пор, пока при некоторой структуре полинома (6.62) и размерности  не выполнится условие
не выполнится условие 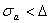 . Подобный процесс построения ММ связан с исключительно большим объемом вычислений, так как структура ММ (6.62) и размерность
. Подобный процесс построения ММ связан с исключительно большим объемом вычислений, так как структура ММ (6.62) и размерность  заранее не заданы и должны быть определены в процессе решения задачи.
заранее не заданы и должны быть определены в процессе решения задачи.
Указанные трудности вычислительного характера могут быть устранены или уменьшены, если для построения ММ сложного объекта применить метод группового учета аргументов (МГУА).
Согласно этому методу решение трудоемкой исходной задачи (как правило, неустойчивой) аппроксимации таблично заданной функции 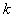 переменных
переменных 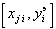 ,
, 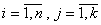 полиномом (6.62), структура которого и размерность
полиномом (6.62), структура которого и размерность 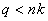 заранее не заданы, заменяется многостадийным процессом решения большого числа сравнительно простых задач аппроксимации табличных данных функциями двух переменных — полиномами заданной структуры с невысокой размерностью вектора
заранее не заданы, заменяется многостадийным процессом решения большого числа сравнительно простых задач аппроксимации табличных данных функциями двух переменных — полиномами заданной структуры с невысокой размерностью вектора  .
.
На каждой из стадий этого процесса производится отбор “наилучших”, в некотором смысле, полиномов, которые используются на следующей стадии в качестве фиктивных аргументов новых полиномов. Подобная процедура построения сложной функции (полинома от полиномов) продолжается до тех пор, пока на какой-либо стадии не будет достигнута приемлемая точность описания свойств объекта (табличных данных) некоторой математической зависимостью 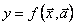 , быть может и меньшего, чем
, быть может и меньшего, чем 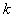 , числа аргументов
, числа аргументов 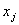 .
.
Рассмотрим подробно первые две стадии этой процедуры.
Пусть задана совокупность (таблица) экспериментальных данных 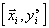 при
при 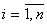 , которую требуется аппроксимировать с допустимой средней квадратической погрешностью
, которую требуется аппроксимировать с допустимой средней квадратической погрешностью  некоторой функцией, число переменных
некоторой функцией, число переменных 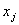 которой меньше или равно
которой меньше или равно 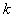 .
.
Разобьем эту совокупность данных на три множества:
обучающее 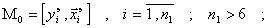
проверочное 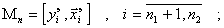
контрольное 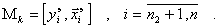
На первой стадии аппроксимации построим 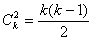 полиномов
полиномов 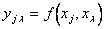 двух аргументов
двух аргументов 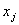 и
и 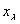 типа
типа 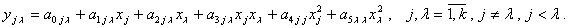 (6.63)
(6.63)
Структура частной модели (6.63) может быть выбрана иная, например, при 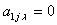 или
или 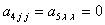 и т.п.
и т.п.
Такие полиномы будем называть частными .
Вектор коэффициентов 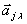 каждого частного полинома определяется МНК по экспериментальным данным
каждого частного полинома определяется МНК по экспериментальным данным 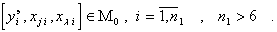
Далее вычислим ординаты каждого частного полином 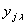 с известными коэффициентами во всех точках
с известными коэффициентами во всех точках 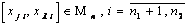 проверочного множества
проверочного множества 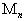 ; обозначим эти данные через
; обозначим эти данные через 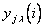 . Средняя квадратическая ошибка
. Средняя квадратическая ошибка 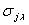 аппроксимации экспериментальных данных
аппроксимации экспериментальных данных 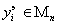 частным полиномом
частным полиномом 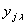 равна:
равна:
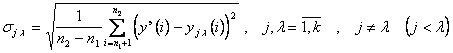 . (6.64)
. (6.64)
Среди всех величин 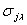 найдем наименьшую и обозначим ее через
найдем наименьшую и обозначим ее через 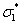 ,
, 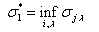 .
.
В соответствии с некоторым правилом отбора, в котором используются величины 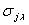 , из всех
, из всех 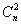 частных полиномов выделим несколько, например,
частных полиномов выделим несколько, например, 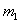 “наилучших” полиномов и переобозначим их через
“наилучших” полиномов и переобозначим их через 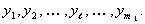
Теперь вычислим значения 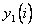 отобранных полиномов во всех точках множеств
отобранных полиномов во всех точках множеств 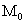 и
и 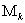 , а также определим СКО
, а также определим СКО 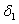 для всех
для всех 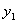 на множестве
на множестве 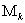
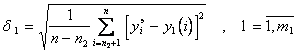 . (6.65)
. (6.65)
Наконец найдем величину
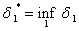 ,
,
которая понадобится на следующих стадиях аппроксимации.
На второй стадии отобранные полиномы 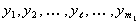 рассматриваются как аргументы новых частных полиномов
рассматриваются как аргументы новых частных полиномов
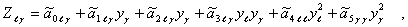 (6.66)
(6.66)
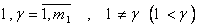 .
.
Количество этих частных полиномов равно числу сочетаний из 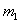 по два
по два
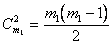 .
.
Коэффициенты 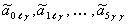 каждого из этих полиномов определяются методом наименьших квадратов по множеству значений
каждого из этих полиномов определяются методом наименьших квадратов по множеству значений 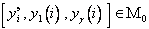 при
при 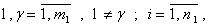 где значения
где значения 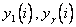 вычисляются во всех точках множества
вычисляются во всех точках множества 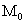 по модели (6.63).
по модели (6.63).
Определим СКО 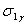 аппроксимации каждым частным полиномом
аппроксимации каждым частным полиномом 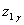 экспериментальных данных
экспериментальных данных 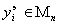 . Для этого подставим полиномы
. Для этого подставим полиномы 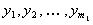 в выражение (6.66), вычислим значения
в выражение (6.66), вычислим значения 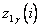 в каждой точке
в каждой точке 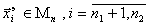 и, аналогично формуле (6.64), найдем
и, аналогично формуле (6.64), найдем 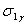 :
:
 (6.67)
(6.67)
Среди всех величин 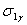 найдем наименьшую и обозначим ее через
найдем наименьшую и обозначим ее через 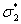 :
:
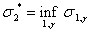 .
.
Далее, в соответствии с принятым правилом отбора, из всех полиномов 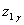 выделим множество “наилучших” полиномов и переобозначим их через
выделим множество “наилучших” полиномов и переобозначим их через 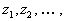
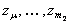 , где
, где 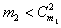 .
.
Каждый полином 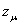 может быть функцией четырех независимых переменных
может быть функцией четырех независимых переменных 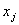 , поэтому вероятность аппроксимации им с приемлемой точностью экспериментальные данные
, поэтому вероятность аппроксимации им с приемлемой точностью экспериментальные данные 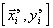 выше, чем на первой стадии. Вследствие этого необходимо выяснить целесообразность перехода к третьей стадии аппроксимации.
выше, чем на первой стадии. Вследствие этого необходимо выяснить целесообразность перехода к третьей стадии аппроксимации. 

Процедура последовательной аппроксимации оканчивается, когда точность приближения независимых экспериментальных данных 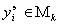 каким-либо “наилучшим” полиномом удовлетворить нашим требованиям. Заметим, что значения
каким-либо “наилучшим” полиномом удовлетворить нашим требованиям. Заметим, что значения 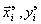 из
из 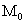 уже использовались для определения коэффициентов полиномов, а данные из
уже использовались для определения коэффициентов полиномов, а данные из 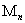 — для отбора “наилучших” полиномов как на первой, так и на второй стадии.
— для отбора “наилучших” полиномов как на первой, так и на второй стадии.
Для проверки точности приближения вычислим сначала значения отобранных полиномов 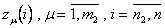 во всех точках множества
во всех точках множества 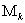 , а затем значения
, а затем значения 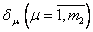 на множестве
на множестве 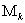 по формуле
по формуле
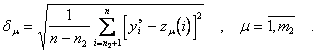 (6.68)
(6.68)
Найдем величину
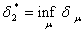 .
.
Если окажется, что 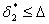 , то соответствующий полином
, то соответствующий полином 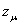 типа (6.66) может рассматриваться как математическая модель сложного объекта. Если же
типа (6.66) может рассматриваться как математическая модель сложного объекта. Если же 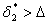 , то необходима третья стадия аппроксимации, на которой в качестве фиктивных аргументов будут выступать
, то необходима третья стадия аппроксимации, на которой в качестве фиктивных аргументов будут выступать 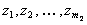 . Значения этих аргументов предварительно вычисляются во всех точках множества
. Значения этих аргументов предварительно вычисляются во всех точках множества 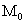 и сводятся в таблицу
и сводятся в таблицу 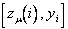 ,
, 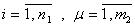 .
.
Во многих случаях допустимая СКО 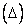 ММ бывает известна весьма неточно и фактически не может быть использована для сравнения с
ММ бывает известна весьма неточно и фактически не может быть использована для сравнения с 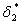 . В таких случаях для окончания процесса аппроксимации можно применять величину
. В таких случаях для окончания процесса аппроксимации можно применять величину
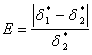 .
.
Если 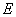 относительно невелика
относительно невелика 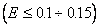 , то дальнейшая аппроксимация малоэффективна и в качестве ММ объекта можно использовать полином
, то дальнейшая аппроксимация малоэффективна и в качестве ММ объекта можно использовать полином 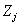 , для которого величина
, для которого величина 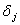 будет наименьшей. Если же
будет наименьшей. Если же 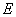 относительно велика, то необходимо третья стадия аппроксимации, вся последовательность расчетов на которой такая же, как и на второй стадии.
относительно велика, то необходимо третья стадия аппроксимации, вся последовательность расчетов на которой такая же, как и на второй стадии.
Приведем еще одно условие окончания процесса аппроксимации, рекомендованное в трудах Ивахненко А.Г.
Практика применения МГУА показывает, что в большинстве случаев с ростом 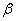 величина
величина 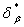 вначале убывает, а затем начинает быстро возрастать. В таких ситуациях необходимо оканчивать процесс последовательной аппроксимации при достижении наименьшего значения СКО
вначале убывает, а затем начинает быстро возрастать. В таких ситуациях необходимо оканчивать процесс последовательной аппроксимации при достижении наименьшего значения СКО 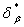 . При этом, оказывается, число стадий
. При этом, оказывается, число стадий 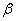 обычно не превышает
обычно не превышает 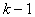 .
.
Дата добавления: 2016-06-22; просмотров: 2576;











