Дробный факторный эксперимент

С увеличением числа факторов количество опытов при ПФЭ растет по показательной функции. В то же время часто заранее известно, что число определяемых коэффициентов в модели объекта намного меньше числа опытов в соответствующем ПФЭ (например, если можно ограничиться линейным приближением модели). В этом случае используя дробный факторный эксперимент (ДФЭ) и получая дробные реплики можно резко сократить число опытов.

ДФЭ позволяет минимизировать число опытов, но при этом оценки коэффициентов получаются смешанными.

Эффективность ДФЭ при определении модели объекта зависит от выбранной системы смешивания. Необходимо выбрать такие дробные реплики, при которых интересующие экспериментатора линейные эффекты смешиваются с теми эффектами взаимодействия, о которых с наибольшей вероятностью можно предположить, что они близки к нулю. Как правило, такое предположение чаще всего справедливо относительно взаимодействий самого высокого порядка.

Для определения системы смешивания оценок используется так называемый определяющий контраст — символическое произведение всех столбцов матрицы планирования равное +1 или -1. Чтобы узнать какие взаимодействия смешаны с данным линейным эффектом (то есть в каких столбцах плана имеются одинаковые элементы) необходимо умножить определяющий контраст на столбец соответствующий данному эффекту.

Положим, что контраст в случае трех факторов равен

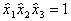. (6.49)

Умножим по очереди определяющий контраст на 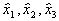, получим

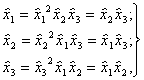(6.50)

поскольку .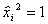

Полученным соотношениям (6.50) соответствует система смешанных оценок:

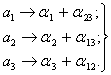(6.51)

При увеличении числа факторов целесообразность использования дробных реплик для получения линейной модели объекта резко возрастает.

Рассмотрим пример ДФЭ. Положим, что интересующая нас модель объекта является функцией трех переменных (факторов), причем заранее известно, что в рабочей области эта модель близка к линейной, то есть

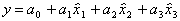(6.52)

При ПФЭ и двух уровнях факторов мы должны осуществить 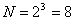опытов. Следовательно, для определения четырех коэффициентов 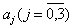модели проводится вдвое больше число опытов.

Используя ДФЭ для решения поставленной задачи можно уменьшить число опытов. Чтобы дробная реплика представляла собой ортогональный план, в качестве реплики следует брать ПФЭ для меньшего числа факторов. Число опытов при этом должно быть больше (или равно) числа неизвестных коэффициентов модели. Следовательно, для рассматриваемого примера можно ограничиться четырьмя опытами. При этом ортогональность плана достигается если использовать план ПФЭ типа 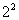, а в качестве плана для 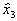использовать столбец 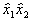. Матрица такого эксперимента приведена в таблице 3.6.

Таблица 3.6

Полуреплика от ПФЭ типа 23

№ опыта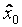
	+	+	+	+
	+	—	+	—
	+	+	—	—
	+	—	—	+

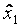
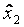
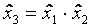
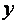
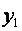
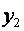
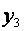
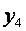
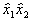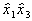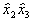Такой сокращенный план (половина ПФЭ) называется полурепликой. Пользуясь таким планированием, можно оценить свободный член и три коэффициента модели при линейных членах. Но если модель объекта не строго линейна и коэффициенты при парных взаимодействиях не равны нулю, то найденные коэффициенты будут смешанными в соответствии с системой (3.50), поскольку элементы столбцов , и (эти столбцы в табл. 3.6 не указаны) совпадают с элементами столбцов 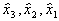соответственно. Если модель объекта действительно близка к линейной, то со смешанностью коэффициентов вполне можно примириться.

По указанному в табл. 3.6 плану проводится половина ПФЭ типа 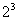и получается полуреплика от 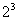, что принято обозначать как 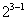. Если знаки одного из элементов столбцов ( 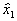, 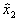или 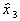) изменить на противоположные, то получим вторую половину ПФЭ (еще 4 опыта) и, следовательно, вторую полуреплику от 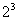. При осуществлении обоих полуреплик мы провели бы ПФЭ 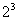(8 опытов) и получили бы раздельные оценки коэффициентов как для линейных эффектов, так и для эффектов взаимодействий.

Пусть 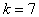, , 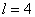тогда план ДФЭ 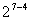включает матрицу плана ПФЭ 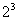для трех факторов 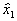, 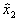и 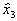, а столбцы плана для остальных факторов представляют собой некоторые произведения факторов 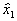, 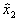и 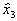, например, 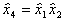, , 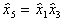, 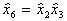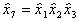. Такие равенства называют генерируемыми соотношениями, их выбор произволен, однако повторение не допускается. При таком планировании все линейные эффекты смешаны с эффектами взаимодействия.

Число опытов в дробной реплике должно удовлетворять неравенству 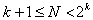, где 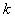— число факторов, для получения несмешанных оценок линейных эффектов.

Если 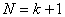, то есть число опытов равно числу определяемых коэффициентов линейной модели, дробная реплика представляет собой насыщенный линейный ортогональный план.

Поскольку число опытов в насыщенных планах равно числу определяемых коэффициентов, число степеней свободы дисперсии адекватности 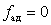. Для поверки адекватности линейной модели, полученной по насыщенному плану, необходим дополнительный эксперимент.

Таким образом оптимальные двухуровневые планы 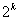и 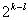имеют следующие преимущества:

 планы ортогональны, и поэтому все вычисления просты, все коэффициенты определяются независимо друг от друга;

 каждый коэффициент определяется по результатам всех 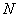опытов;

 для данного числа опытов 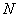эти планы имеют минимальный определитель ковариационной матрицы 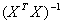; в связи с этим все коэффициенты определяются с одинаковой и минимальной дисперсией, то есть планы обладают свойством Д-оптимальности;

 линейные планы 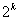и 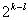обладают свойством ротатабельности.

Покажем справедливость свойства ротатабельности в случае линейной модели

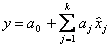. (6.53)

Вследствие отсутствия корреляции между коэффициентами по закону сложения дисперсий для линейной модели (6.53) имеем:

.

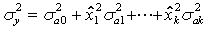Так как 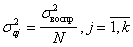, получим

;

,

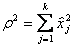где 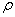— радиус сферы в К-мерном пространстве.

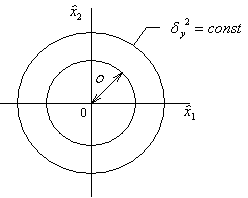
Рис. 3.3.

Дисперсия выхода 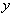растет пропорционально квадрату радиуса сферы 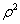и одинаково для всех эквидистантных точек (рис. 3.3).

Планирование обладающее таким свойством называется ротатабельным планированием.

Учет влияния помех

При постановке многофакторного эксперимента на реальном объекте необходимо спланировать его так, чтобы иметь возможность отфильтровать помехи. С этой целью каждый опыт в матрице планирования повторяется в 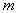раз (табл. 3.7). Обычно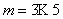

Таблица 3.7

ПФЭ типа 2k

№ опыта				.....
	+	+	+		+
	+	—	+		+
	+	+	—		+
.	.	.	.		.	.	.	.
.	.	.	.		.	.	.	.
.	.	.	.		.	.	.	.
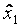
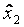
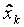
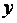
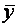
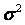
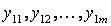
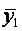
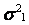
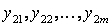
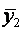
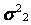
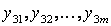
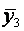
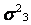
N	+	—	—		—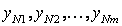

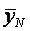
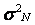
В каждой строчке матрицы планирования определяются среднее значение и дисперсия выхода объекта по 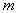параллельным опытам:

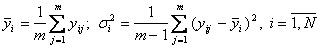, (6.54)

где 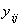— j-ое значение выхода объекта в i-ом опыте.

Проверяется однородность выборочных дисперсий (воспроизводимость эксперимента) по критерию Кохрена. Для этого определяется отношение максимальной дисперсии к сумме всех дисперсий:

(6.55)

Полученное отношение сравнивается с табличным значением (определяется из таблицы распределения Кохрена) 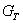при заданной доверительной вероятности 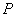и числе степеней свободы .

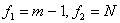Если 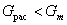дисперсии 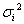однородны (опыты воспроизводимы), в противном случае добиваются достижения однородности дисперсий 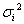, как правило, путем увеличения числа повторных опытов .

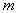Тогда в качестве оценки для дисперсии воспроизводимости

можно взять среднюю дисперсию

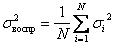(6.56)

с числом степеней свободы .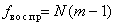

Коэффициенты модели определяются изложенным в разделе 3.2.3 способом. При этом в формулах (6.34), (6.36), (6.37) для вычисления коэффициентов следует вместо 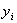принимать значение 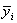. Например, коэффициенты линейных эффектов определяются по формуле

.

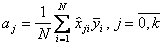Упрощение модели путем отсеивания ее незначимых коэффициентов осуществляется по критерию Стьюдента (раздел 6.2.4), а проверка адекватности модели — по критерию Фишера (раздел 6.2.5). Однако, в данном случае необходимо учитывать следующее. Дисперсия воспроизводимости определяется по формуле (6.56). Учитывая, что дисперсия среднего 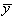, полученного по выборке объема 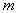, в 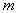раз меньше дисперсии единичного измерения 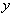, то есть

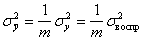, (6.57)

в рассматриваемом случае дисперсия коэффициентов 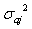определяется следующим образом:

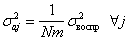. (6.58)

В матрице планирования каждый опыт повторялся в 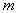раз. Поэтому дисперсию адекватности нужно умножить на 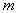, то есть

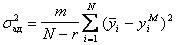. (6.59)

Незначимые коэффициенты отсеиваются из уравнения регрессии. При этом ввиду ортогональности матрицы планирования остальные коэффициенты не приходится пересчитывать. В случае же не подтверждения адекватности модели необходимо увеличить порядок аппроксимирующего полинома.

Необходимость повышения порядка модели может определяться также исходя из следующего соображения. На практике часто оказывается, что линейная модель, адекватно описывающая опытные данные, поставленные в точках плана, неудовлетворительно характеризует внутреннюю часть изученной области факторного пространства. Поэтому имеет смысл поставить опыт в центре плана 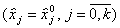. Среднее значение выхода объекта в центре плана должно быть соизмеримо (в пределах ошибки воспроизводимости) с коэффициентом a0 модели, то есть

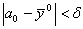, (6.60)

где 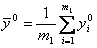, 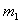— число повторных опытов в центре плана, 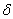— малое число.

В случае нарушения условия (6.60) для математического описания рассматриваемой области факторного пространства потребуется уравнение более высокого порядка.