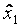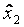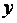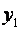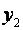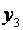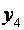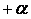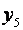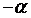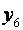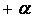Построение модели с квадратичными эффектами

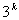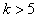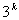Построение модели, содержащую степени факторов, требует иметь такую систему планирования, в которой каждый фактор будет принимать хотя бы три разных уровня. ПФЭ типа содержит слишком большое число опытов. При ПФЭ становится совершенно неприемлемым для практики.

Сократить число опытов можно, если воспользоваться композиционными или последовательными планами, предложенными Боксом и Уилсоном. Ядро таких планов составляет ПФЭ 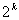при 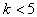или полуреплика от него ДФЭ 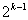при 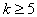. Возможность использования в качестве ядра плана 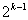при 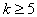обусловлена тем, что уже полуреплика обеспечивает получение несмешанных оценок для линейных эффектов и эффектов парного взаимодействия.

Если линейная модель (а также модель с эффектами взаимодействия) оказалась неадекватной, необходимо:

1) добавить 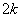звездных точек, расположенных на координатных осях факторного пространства. Координаты звездных точек:

,

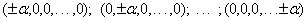где 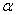— расстояние от центра плана до звездной точки (звездное плечо);

2) увеличить число опытов 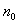в центре плана.

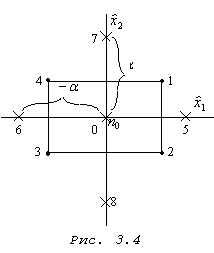
Рассмотрим построение композиционного плана при 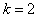(рис. 3.4). Точки 1 — 4 образуют ПФЭ 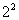, точки 5 — 8 — звездные точки с координатам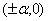и и 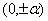, координаты 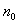опытов в центре плана нулевые — .

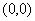Общее число опытов в матрице композиционного плана второго порядка при 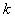факторах:

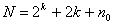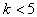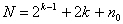при ;

при .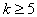

Матрица плана приведена в табл. 3.8. Композиционные планы легко приводятся к ортогональным выбором соответствующего звездного плеча 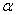. На количество опытов в центре плана 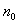при этом не накладывается никаких ограничений (обычно 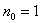). При этом достаточно определить 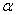из условия:

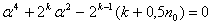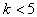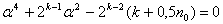при ;

при .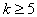

Таблица 3.8 Матрица композиционного плана № опыта +1 +1 -1 +1 +1 -1 -1 -1 . . . . . . . . N

Благодаря ортогональности матрицы планирования все коэффициенты модели определяются независимо друг от друга по формулам:

;

;

;

,

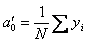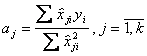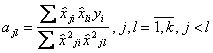где суммирование всюду осуществляется по 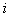от 1 до N.

В результате расчетов по ортогональной матрице с преобразованными столбцами для квадратичных эффектов получим уравнение вида

.

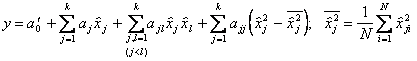Чтобы перейти к обычной записи коэффициент 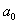определяют по формуле:

.

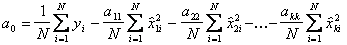В результате получим уравнение вида

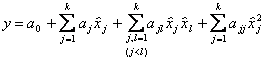. (6.61)

Коэффициенты модели, получаемые при помощи ортогональных планов второго порядка, определяются с разной точностью. Поэтому для расчета оценки дисперсий коэффициентов 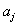используют следующие выражения:

;

;

;

.

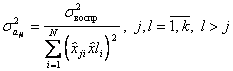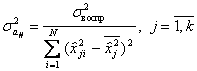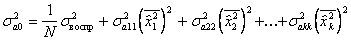Дисперсия 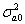получена по закону сложения дисперсий.

После вычисления коэффициентов проверяют значимость коэффициентов по критерию Стьюдента и адекватность модели по критерию Фишера.

Следует отметить, что ортогональные планы второго порядка не обладают свойством ротатабельности, что является их недостатком. Однако простота всех вычислений оставляет за ортогональными планами право на существование.