Аналитическая оценка характеристик антенного окна в условиях нагрева

Оценка в виде расчетных формул возможна, но полученные формулы справедливы для очень упрощенных условий нагрева. Кроме того, зачастую мы не знаем исходные данные для расчета. Расчетные формулы – это довольно громоздкая электродинамика, поэтому записывать их не будем.

Представим себе, как ставится электродинамическая задача. Изобразим антенное окно:

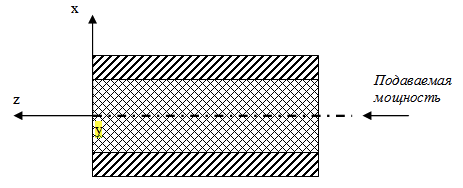
На рисунке изображен волновод круглого сечения, заполненный в торце диэлектриком. В таком волноводе распространяется стандартный тип волн Н₁₁. Для разговора выбрана декартова система координат. Излучение происходит в направлении оси Z. Ось Y смотрит на нас. Плоскость X0Y – плоскость апертуры антенны.

Нам изначально известны:

- размеры волновода, поскольку знаем длину волны в волноводе (или рабочую частоту);

- электрические характеристики диэлектрика при температуре 20 градусов Цельсия;

- распределение поля в излучателе (волноводе), который мы знаем благодаря типу колебаний Н₁₁;

- толщина вставки из диэлектрика.

Рассмотрим простейший случай для следующих допущений:

1) вставка однородная и изотропная (при нагреве условие однородности нарушается);

2) изменение поля во времени гармоническое;

3) поле плоское;

4) поле однородное.

Используем волновое уравнение Максвелла для компоненты поля Н.

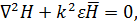
где k – постоянная вихревых токов, волновое число,

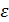– диэлектрическая проницаемость среды, в которой рассматриваем поле.

Аналогичную запись можно сделать для компоненты Е.

В векторном виде это уравнение не решаем, а переходим к скалярному виду уравнений в виде проекций на оси X и Y (для E, H компоненты). Проекции на ось Z не будет, так как в направлении этой оси направлен вектор Умова-Пойтинга.

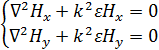
Распишем проекцию волнового уравнения для оси Х.

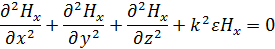
Для неоднородной среды .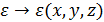

Уравнение 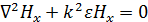может быть решено, если поле плоское. Однако, как правило, мы работаем с цилиндрическим (или сферическим) полем. Поэтому используют подход, называемый угловым спектром плоских волн. Идея состоит в следующем – сферическое излучение, неплоская неоднородная волна, представляется набором плоских волн, каждая из которых распространяется под своим углом и представляет собой отдельный луч со своей амплитудой. Таких лучей бесконечно много. Отсчет луча ведем от оси излучения антенны. Если уже говорим о луче, нет проблем ни с плоскостью, ни с однородностью.

Угловой спектр поля Н можно записать как прямое преобразование Фурье структуры поля для волны Н₁₁ (т.е. напряженности поля Н):

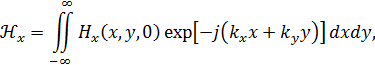
где	kx, ky – проекции волнового вектора на оси X, Y; 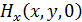означает, что рассматриваем напряженность в начале координат (в начале антенной вставки).

Если выполним данное ППФ, то получим отсутствие зависимости от координат, а соотношение проекций даст угол по отношению к оси Z.

Такое же выражение можно записать и для углового спектра для проекции на ось «y» .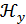

После интегрирования мы получаем зависимость не от координат, а от соотношений проекций (т.е. угла по отношению к оси Z).

После ППФ можем перейти к волновым уравнениям для волнового спектра плоских волн и записать его следующим образом:

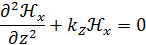
Решение этого уравнения в общем виде:

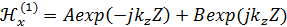
Почему здесь два слагаемых? Здесь нужно отметь, что мы имеем две среды, в которых происходит излучение из круглого волновода:

- теплозащита (пространство, занимаемое антенной вставкой) (1);

- среда за теплозащитой (воздух, плазма) ⁽²⁾.

Знак в экспоненте говорит о направлении переноса энергии. У нас разные знаки в двух слагаемых, значит, разное направление, а такое может происходить только при отражении от границы раздела между теплозащитной вставкой и средой.

Первое слагаемое характеризует волну падающую, распространяющуюся в антенной вставке, тогда как второе слагаемое – волна отраженная от границы раздела.

Таким образом, общее решение, записанное выше, записано для первой среды, т.е. для теплозащиты.

Для второго случая, т.е. для среды за теплозащитой, будет только падающая волна, поэтому имеем право записать:

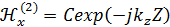
Сделаем ещё одно уточнение. k_z – проекция волнового вектора на ось Z, которую можем определить таким образом:

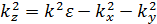
В это выражение входит диэлектрическая проницаемость среды. Когда мы говорим о первой среде (об антенной вставке), надо учитывать, что у нее будет своё значение диэлектрической проницаемости 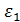. Поэтому имеем право записать:

· для первой среды ;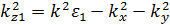

· для второй среды ( .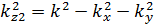

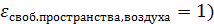Нас интересуют частные решения для нашего конкретного случая, т.е. должны найти постоянные интегрирования, которые могут быть абсолютно любыми. Однако мы должны использовать граничные условия для координаты Z (z=0; z=d, где d – толщина антенной вставки; z= ).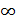

Найдя в конкретном виде постоянные интегрирования, получим угловой спектр плоских волн для иксовой проекции напряженности поля H.

Отметим отдельно, что сутью всех этих вычислений было нахождение характеристик антенны – диаграммы направленности, КПД, шумовой температуры антенны.

Диаграмма направленности – распределение в пространстве напряженности поля излучения. Также диаграмма направленности может быть получена для мощности излучения. Обычно её получают для электрической составляющей поля Е.

Зная результат спектра и используя обратное преобразование Фурье, от 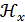вернемся к :

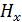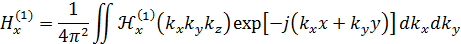
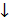
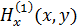
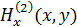
Мы должны найти распределенность поля для второй среды (среды за антенной вставкой) 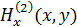. Интегралы можно найти не для всех распределений поля. В конечном итоге осталось перейти к электрической компоненте Е по уравнениям Максвелла и найти .

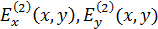Можно перейти от декартовых координат к сферическим:

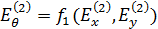
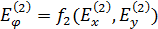
Эти формулы будут приближенными в силу сделанных допущений по свойствам среды.

КПД 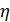– отношение полезной мощности к потребленной. Полезная мощность антенны – это мощность излучения.

Потребленную мощность нам не надо искать – это та мощность, которую подводим к антенне. Излученная мощность – это квадрат распределенности поля:

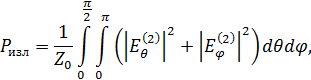
где Z₀ – волновое сопротивление среды, на которую мы излучаем.

Шумовая температура антенны – не аналитическая величина, а эмпирическая.