Проверка адекватности модели

Полученную с помощью факторного планированного эксперимента модель объекта необходимо проверить на адекватность. Это осуществляется с помощью критерия Фишера (при наличии степеней свободы):

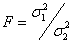, (3.44)

где 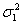, 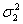— дисперсии двух независимых выборок.

При расчете 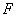— критерия в числитель ставят большую из двух эмпирических дисперсий, поэтому 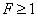. Критерий Фишера показывает значимо ли отличаются друг от друга эти дисперсии.

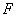— критерий формируют следующим образом:

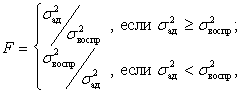(6.45)

где 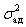— дисперсия адекватности (остаточная дисперсия).

Дисперсия воспроизводимости вычисляется по формуле (6.41), а дисперсия адекватности по формуле

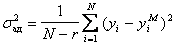, (6.46)

где 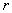— число значимых коэффициентов модели;

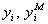— экспериментальные отклики и отклики, рассчитанные по модели при тех же значениях факторов.

Число степеней свободы для дисперсии адекватности

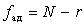. (6.47)

Для 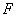-критерия имеются специальные таблицы распределения Фишера, рассчитанные для различных 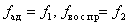и доверительных вероятностей 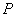(уровней значимости 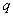). Если

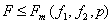, (6.48)

то с соответствующей доверительной вероятностью 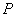можно принять, что 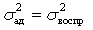и считать модель в исследованной области адекватной объекту.

Таким образом, с помощью 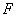-критерия проверяется лишь тот факт, что дисперсия адекватности не отличается значимо от дисперсии воспроизводимости, то есть ошибка модели и ошибка связанная с точностью эксперимента, на основе которого построена модель, близки друг другу. Этого достаточно для утверждения, что полученная модель адекватно описывает результаты эксперимента.

Если 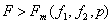, то для адекватного описания эксперимента необходимо увеличить порядок модели (например, ввести в модель квадраты факторов). В этом случае эксперимент проводится при числе уровней факторов больше чем 2.

Для случаев, когда повторные опыты ставятся во всех (или в нескольких) точках плана одинаковое или неодинаковое число раз, формулы (3.41) и (3.46) несколько изменяются.