Уравнение гармонической бегущей волны
Волновые свойства упругих и электромагнитных волн
Лекция 1. Волны в упругих средах
В первой части курса были рассмотрены простейшие случаи механических колебаний. При этом мы не интересовались процессами, происходящими в среде, окружающей колебательную систему. Сейчас мы обратим на это внимание.
Упругие среды. Продольные и поперечные волны
Будем полагать, что имеем сплошную упругую среду, например, твердое тело, жидкости, газы. Для упругой среды характерно возникновение упругих деформаций при внешнем воздействии на нее. Эти деформации полностью исчезают после прекращения внешних воздействий.
Если в каком-либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться в среде с некоторой скоростью v.
Процесс распространения колебаний в среде называется волной. Иначе, возмущение, распространяющееся в пространстве (среде), называется волной.
Механические возмущения (деформации), распространяющиеся в упругой среде, называются упругими или механическими волнами.
Звуковыми или акустическими волнами называются упругие волны, обладающие частотами в пределах 16-20000 Гц. Волны с частотами меньше 16 Гц (инфразвук) и больше 20000 Гц (ультразвук) органами слуха человека не воспринимаются.
Упругие волны бывают продольныеипоперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в твердых, жидких и газообразных средах. Поперечные волны могут возникать только в твердых телах.
Отметим, что распространение упругих волн не связано с переносом вещества. Бегущие волны переносят энергию колебательного движения в направлении распространения волны.
Уравнение гармонической бегущей волны
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими, т.е. описываются по закону синуса или косинуса. Часто гармоническую волну называют синусоидальной.
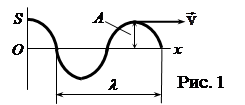 На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х этих частиц от источника колебаний О для фиксированного момента времени t.
На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х этих частиц от источника колебаний О для фиксированного момента времени t.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространится гармоническая волна за время, равное периоду колебаний Т, т.е.
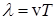 . (1)
. (1)
Учитывая, что частота v = 1/T получаем
l = v / v. (2)
т.е. длина волны обратно пропорциональна частоте.
Уравнение такой волны в общем случае имеет вид
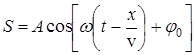 , (3)
, (3)
Для характеристики волн используется волновое число
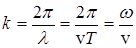 , (4)
, (4)
где w = 2p/T = 2pv – циклическая, (круговая) частота.
С учетом (4) получим уравнение бегущей гармонической волны
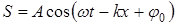 , (5)
, (5)
где А – амплитуда волны, 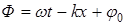 – фаза волны, j0– начальная фаза.
– фаза волны, j0– начальная фаза.
Основываясь на формуле Эйлера (  ), уравнение (5) можно записать в экспоненциальной (комплексной) форме
), уравнение (5) можно записать в экспоненциальной (комплексной) форме
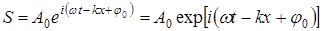 , (6)
, (6)
где физический смысл имеет лишь действительная часть выражения (6). Такая форма представления волны существенно облегчает математический действия.
Дата добавления: 2016-06-22; просмотров: 5461;











