Лекция 2. Электромагнитные волны

Во второй части курса физики изучались уравнения Максвелла, которые в дифференциальной форме (т.е. справедливые для бесконечно малого объема среды) имели вид:

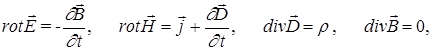(1)

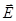где и 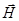– векторы напряженности электрического и магнитного полей, которые измеряются соответственно в В/м и А/м; 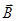– вектор магнитной индукции (Тл), 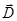– вектор электрического смещения (Кл/м²), 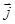– вектор плотности тока проводимости (А/м²), r – объемная плотность заряда (Кл/м³).

Кроме того, необходимо учитывать, что

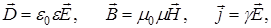(2)

где e₀=1/(4p×9×10⁹) Ф/м, m₀=4p×10^-7Гн/м – электрическая и магнитная постоянные; ε, μ – диэлектрическая и магнитная проницаемости среды; g – удельная электропроводность среды (величина, обратная удельному сопротивлению), а также, что

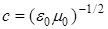, (3)

c – скорость света в вакууме, с = 3×10⁸ м/с.

Скорость распространения электромагнитных волн в среде

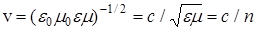, (4)

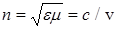где , (5)

n – абсолютный показатель преломления среды, он показывает, во сколько раз скорость света v в среде меньше скорости света в вакууме с.

Из первого уравнения Максвелла следует, что переменное (изменяющееся во времени) магнитное поле вызывает переменное электрическое поле, а оно [согласно второму уравнению (1)], изменяясь, вызывает магнитное поле и т.д. Нельзя создать только электрическое поле, не вызвав магнитного поля и наоборот. Т.е. электрическое и магнитное поля взаимосвязаны. Они образуют единое электромагнитное поле, которое распространяется в пространстве (среде) в виде электромагнитных волн.

Волновые уравнения

Электромагнитные волны удовлетворяют уравнениям аналогичным (1.9)*, которые выводятся из уравнений Максвелла с применением векторного равенства

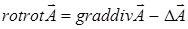
Для линейной однородной изотропной среды при отсутствии токов ( 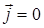) и зарядов (r=0) волновые уравнения для векторов 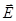и 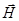имеют вид

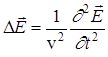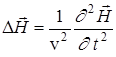, , (6)

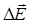где и 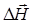– операторы Лапласа, примененные к векторам 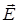и 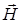соответственно, они выражаются через операторы Лапласа от скалярных функций

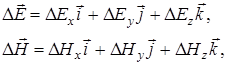(7)

где 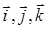– единичные векторы (орты).

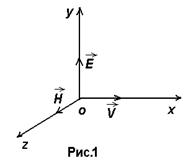В (1.10) приведено выражение для оператора Лапласа, примененного к скалярной функции. Будем далее предполагать, что электромагнитная волна распространяется в направлении оси x (см. рис. 1) со скоростью 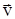и при этом вектор 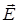колеблется в одной плоскости, например, в плоскости xoy (эту плоскость называют плоскостью поляризации). Тогда вектор 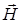будет колебаться в перпендикулярной к ней плоскости xoz [это следует из двух первых уравнений (1)], т.е. в такой линейно поляризованной волне векторы 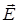и 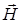имеют только по одной составляющей, т.е. .

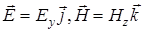Следует заметить, что векторы 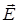, 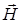и 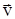образуют правую тройку взаимноперпендикулярных векторов (т.е. направление вектора 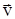совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от 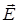к 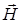по наикратчайшему пути).

Для такой линейно поляризованной волны волновые уравнения (6) упростятся и примут вид

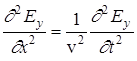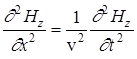, , (8)

где индексы y и z при Е и Н подчеркивают лишь то, что векторы 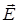и 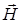направлены вдоль взаимно перпендикулярных осей y и z.