P-поляризация падающей электромагнитной волны.

Плоскость колебаний вектора напряжённости электрического поля 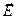падающей электромагнитной волны лежит в плоскости падения. Величина и ориентация волновых векторов падающей, отраженной и преломлённой волны определяются дисперсионным уравнением и условиями периодичности вдоль координатных осей, лежащих в плоскости раздела диэлектрик-проводник. 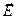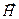Эти соотношения не зависят от величины амплитуд векторов или , поэтому ниже полагаем справедливыми соотношения (9), (10) , (18), (27) и (28). 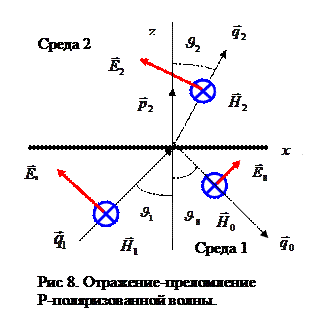В случае s-поляризации нам удалось записать компоненты напряженности электрического поля падающей, отражённой и преломлённой волн, которые удовлетворяли условиям ортогональности (3): векторы 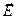имели одну единственную проекцию разной величины. Векторы напряжённости магнитного поля 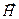лежали в плоскости падения. В рассматриваемом случае удобно задать векторы 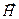как векторы, перпендикулярные плоскости падения, а для определения векторов напряжённости электрического поля 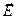использовать уравнение (6).

Итак, поле падающей волны опишем соотношениями:

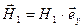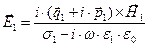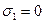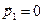, , , . (40)

Поле отражённой волны имеет такую же форму:

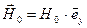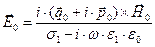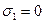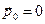, , , . (41)

Поле преломлённой волны формируется с помощью вектора 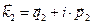, у которого мнимая составляющая не обращается в нуль:

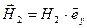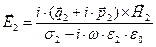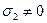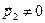, , , . (42)

Развёрнутая покоординатная форма записи выражений для компонент векторных амплитуд напряжённости электрического поля имеет вид:

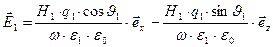, (43)

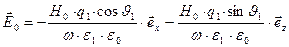, (44)

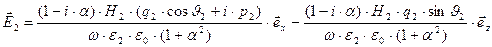. (45) Легко проверить, что комплексные векторы Умова-Пойнтинга для падающей, отражённой и преломлённой волн лежат в плоскости падения и направлены параллельно соответствующим волновым векторам.

Потребуем выполнения условий сопряжения на границе раздела двух сред. Условие непрерывности касательных компонент векторов напряжённости электрического поля в проекции на ось х приводит к уравнению:

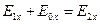. (46)

Условие непрерывности касательных компонент векторов напряжённости электрического поля в проекции на ось у выполнено автоматически: все проекции равны нулю по построению. Таким же образом убеждаемся, что касательные компоненты векторов напряжённости магнитного поля в проекции на ось х непрерывны, они тоже равны нулю по построению. Условие непрерывности касательных компонент векторов напряжённости магнитного поля в проекции на ось у в предположении, что на границе раздела отсутствуют поверхностные токи проводимости, приводит к уравнению:

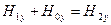. (47)

В систему уравнений (46)-(47) подставим явные выражения для всех задействованных величин и решим эту систему относительно амплитуд магнитного поля отражённой и преломлённой волн 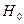и 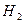, полагая известной величиной амплитуду магнитного поля падающей волны :

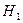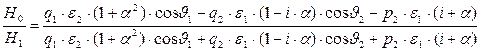, (48)

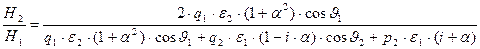. (49)

Теперь векторы 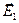, 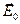и 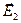полностью определены. Для удобства сравнения полученных результатов с результатами классических руководств по оптике (монография М.Борна и Э.Вольфа «Основы оптики» или учебник Д.В. Сивухина «Оптика», курс общей физики, том 4.) вычислим «длину» (скалярную амплитуду) каждого вектора 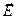по формуле:

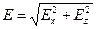(50)

и найдём отношения скалярной амплитуды отражённой волны к скалярной амплитуде падающей волны, скалярной амплитуды преломлённой волны к скалярной амплитуде падающей волны:

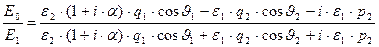, (51)

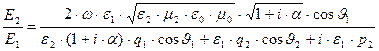. (52)

Комплексные правые части выражений (51)-(52) можно записать в форме произведения модуля комплексной величины на фазовый множитель – экспоненту с мнимым аргументом. Наличие фазового множителя определяет скачок фазы колебаний соответствующей физической величины по отношению к фазе колебаний аналогичной величины в падающей волне.

Соотношения (51)-(52) в результате предельного перехода 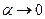(отсутствие проводимости второй среды) приобретают вид:

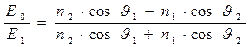, (53)

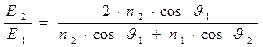. (54)

При выводе соотношений (53)-(54) предполагалось 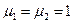, , 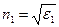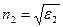. Соотношения (53) и (54) совпадают с аналогичными соотношениями для формул Френеля для отражения-преломления электромагнитной волны на границе двух диэлектриков. Заметим, что явление отражения-преломления электромагнитной волны на поверхности радела диэлектрик-диэлектрик не сопровождается скачком фаз колебаний: фазы колебаний физических величин падающей, отражённой и преломлённой волн совпадают между собой.

Соотношение (53) в результате тригонометрических преобразований и использования классического закона Снеллиуса можно привести к виду

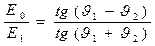. (55)

При выполнении вполне реального условия 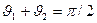знаменатель зависимости (55) обращается в бесконечность, при этом 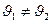, вследствие чего отношение амплитуд отражённой и падающей волны становится равным нулю: исчезает отражённая волна Р-поляризации. Описанный эффект носит название явление Брюстера, а угол падения, при котором он наблюдается, называют углом Брюстера:

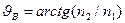. (56)

При отражении-преломлении электромагнитной волны S-поляризации на границе раздела диэлектрик – проводящая среда 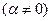интенсивность отражённой волны в ноль не обращается ни при какой величине угла падения. Действительно, рассмотрим результаты расчётов зависимости квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны Р-поляризации для нескольких значений относительного показателя преломления 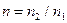и при заданной величине параметра проводимости 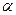второй среды (рис.9).

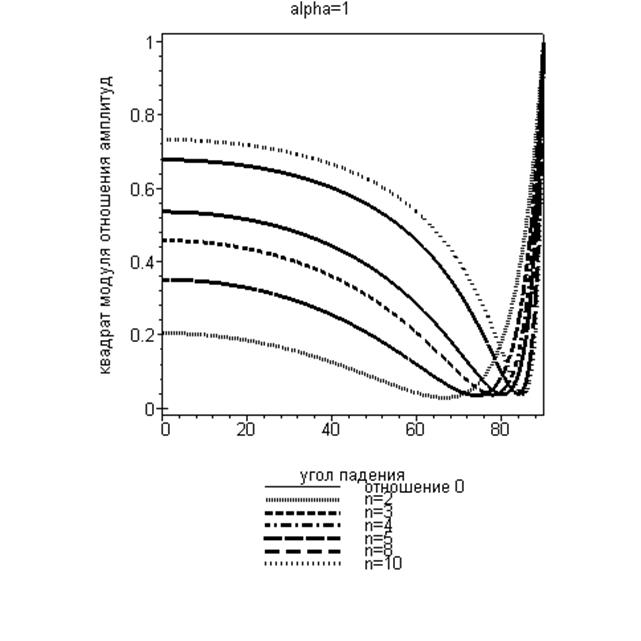
Рис. 9. Зависимость квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны Р-поляризации (параметр проводимости ) для нескольких значений относительного показателя преломления n.

На рисунке 9 отчётливо проявился немонотонный характер исследуемой зависимости от угла падения и принципиальная невозможность обращения в нуль квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны Р-поляризации, хотя имеется значение угла падения, при котором это отношение минимально. Интересно, что описанное минимальное значение практически не зависит от величины относительного показателя преломления, а определяется только величиной параметра проводимости второй среды.

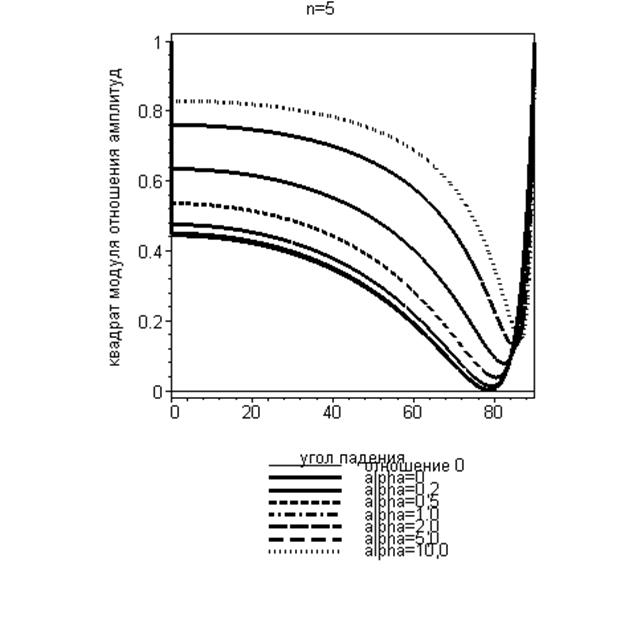
Рис.10. Зависимость квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны Р-поляризации при различных значениях параметра проводимости и фиксированном значении относительного показателя преломления (n=5).

Графики зависимости квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны Р-поляризации от угла падения при различных значениях параметра проводимости и фиксированном значении относительного показателя преломления (n=5) приведены на рис.10. На этом рисунке, в частности, показан случай классического явления Брюстера как частный случай общего явления отражения-преломления электромагнитной волны Р-поляризации на границе раздела диэлектрика и проводника.

Численные расчёты углов преломления и амплитудных отношений по результатам настоящего рассмотрения совпадают с результатами расчётов по известным соотношениям М.Борна. Однако, рассмотрение проблемы преломления электромагнитной волны Р-поляризации можно будет считать законченным, если окажутся выполненными все физические условия на границе раздела сред. Условия непрерывности касательных компонент векторов напряжённости электрического и магнитного поля были обсуждены и использованы при построении решения. Нормальные к поверхности раздела компоненты вектора магнитной индукции равны нулю по построению решения – условие их непрерывности выполнено. Остаётся рассмотреть условие скачка нормальных компонент вектора 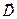при переходе через границу раздела:

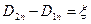, (57)

где 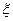- поверхностная плотность сторонних электрических зарядов на поверхности раздела. Это условие необходимо рассматривать совместно с условием сохранения электрического заряда на поверхности раздела:

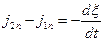, (58)

которое мы записываем в предположении отсутствия поверхностных токов проводимости ( 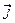- вектор объёмной плотности тока проводимости). Напомним, что положительное направление нормали к поверхности раздела сред совпадает с направлением оси z декартовой системы координат, первая среда находится ниже поверхности раздела, а вторая – выше.

Перепишем уравнение (55) с использованием материальных уравнений среды:

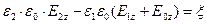. (59)

Уравнение (58) преобразуем с учётом дифференциальной формы закона Ома и условия гармонического характера изменения поверхностной плотности сторонних электрических зарядов с течением времени:

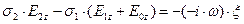. (60)

Комбинируя уравнения (59) и (60), приходим к соотношению:

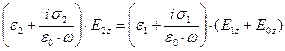. (61)

Если вспомнить определение комплексной диэлектрической проницаемости 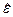, широко используемое при рассмотрении электромагнитных гармонических волн в проводящей среде,

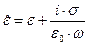, (62)

условие (61) можно записать в форме

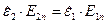. (63)

Это условие используется в многочисленных учебных пособиях и монографиях, как правило, формально, без объяснения физического содержания и без детального обоснования правильности. Проведённые выкладки показывают, что таким образом записанное условие «непрерывности» нормальных компонент 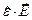объединяет в себе два закона и справедливо оно только для гармонического приближения.

Интересным физическим результатом рассмотрения преломления Р-поляризованной электромагнитной волны на границе диэлектрик-проводник является обнаружение поверхностной плотности сторонних электрических зарядов на поверхности раздела и отсутствие поверхностной плотности токов проводимости.

В заключение отметим, что распространённое в учебной литературе описание явления отражения-преломления электромагнитной волны на поверхности раздела диэлектрик-проводник с использованием априори комплексной диэлектрической проницаемости и формальной аналогии со случаем непроводящих сред содержит математические выражения, не имеющие ясного геометрического содержания и, вообще говоря, физического обоснования. В этом отношении дело обстоит также как и с исходными формулами Френеля двухсотлетней давности в теории эфира: посылки сомнительны, а результат удивительно правильный.

По результатам расчёта отношений скалярных амплитуд напряжённости электрического поля можно вычислить интенсивность волны, отражённой от поверхности проводника. Эту величину можно измерить экспериментально. Последнее позволяет определить «динамические» значения диэлектрической проницаемости проводника, которые часто сильно отличаются «статических» величин.