Энергия бегущей волны. Вектор плотности потока энергии

Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны (5)

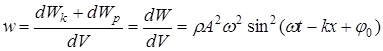, (15)

где r=dm/dV – плотность среды, т.е. периодически изменяется от 0 до rА²w² за время p/w=Т/2.

Среднее значение плотности энергии за промежуток времени p/w=Т/2

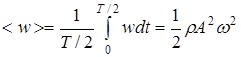. (16)

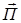Для характеристики переноса энергии вводят понятие вектора плотности потока энергии – вектор Умова.

Выведем выражение для него.

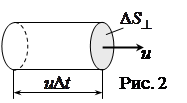
Если через площадку DS_^, перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии

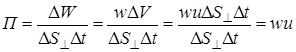, (17)

где DV=DS_^ uDt – объем элементарного цилиндра, выделенного в среде.

Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора

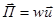, Вт/м². (18)

Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г.

Среднее значение его модуля называют интенсивностью волны

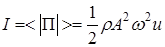. (19)

Для гармонической волны u=v[cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v.

Стоячие волны

Если навстречу друг другу распространяются две гармонические волны 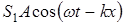и 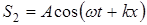, то образуется стоячая волна

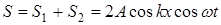. (20)

Исследуем сначала множитель coskx=cos2px/l. В точках x=±(1+2n)l/4, где n=0,1,2..., coskx=0и, следовательно, S=0. Эти точки не колеблются и поэтому называются узлами стоячей волны (см. рис.3). Расстояние между соседними узлами равно l/2. Точки максимальной амплитуды стоячей волны называются пучностями. Их координаты x=±nl/2. Расстояние между соседними пучностями равно l/2.

На рис. 3 сплошной линией изображена зависимость 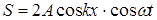от х, соответствующая моменту времени t (например, t=0), при котором coswt= cos2pt/T=1. Через четверть периода cos 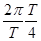=0и S=0. Еще через время, равное T/4, cos 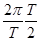= -1, и соответствующая зависимость S от х изображена штриховой линией (см. рис. 3). Спустя t=3T/4 S=0 и через t=T все повторится.

В случае стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут энергию в противоположных направлениях. Т.о., стоячая волна характеризует колебательное состояние среды.

В заключении отметим, что несмотря на разнообразие волновых явлений, они описываются одинаковыми законами (математичеcкими уравнениями). Это позволяет, например, перенести полученные в данной лекции закономерности для упругих волн на электромагнитные волны.