P-поляризация падающей волны
Падающая электромагнитная волна является 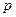 - поляризованной, если вектор напряжённости электрического поля волны лежит в плоскости падения. Поскольку в падающей волне векторы напряжённости электрического и магнитного поля взаимно ортогональны и ортогональны по отношению к волновому вектору падающей волны, анализ рассматриваемого случая удобно провести, если задать пространственную ориентацию вектора напряжённости магнитного поля: пусть вектор
- поляризованной, если вектор напряжённости электрического поля волны лежит в плоскости падения. Поскольку в падающей волне векторы напряжённости электрического и магнитного поля взаимно ортогональны и ортогональны по отношению к волновому вектору падающей волны, анализ рассматриваемого случая удобно провести, если задать пространственную ориентацию вектора напряжённости магнитного поля: пусть вектор 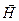 будет параллелен оси
будет параллелен оси 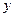 , как это было с вектором
, как это было с вектором 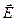 в случае
в случае 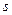 - поляризации падающей волны.
- поляризации падающей волны.
Волновые векторы падающей, отражённой и преломлённой волн, введённые выше, остаются неизменными и в рассматриваемом случае.
Итак, для электромагнитного поля падающей волны имеем:
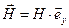 .
.
Используя уравнения (3) и определение волнового вектора
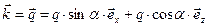 ,
,
получим выражения для комплексной амплитуды вектора напряжённости электрического поля:
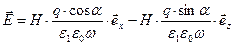 .
.
Для отражённой волны положим
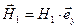
и с учётом выражения для волнового вектора
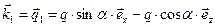
получим комплексную амплитуду вектора напряжённости электрического поля:
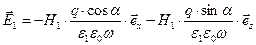 .
.
Аналогичным образом определим параметры преломлённой волны
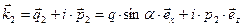 ,
,
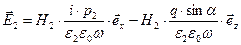 .
.
Рассмотрим условия сопряжения электромагнитного поля на границе раздела сред. Непрерывность касательных компонент векторов напряжённости магнитного поля в проекции на ось 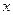 выполняется вследствие принятых выше определений ориентации этих векторов. Условие непрерывности касательных компонент векторов напряжённости магнитного поля в проекции на ось
выполняется вследствие принятых выше определений ориентации этих векторов. Условие непрерывности касательных компонент векторов напряжённости магнитного поля в проекции на ось 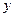 приводит к уравнению:
приводит к уравнению:
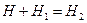 .
.
Условие непрерывности касательных компонент векторов напряжённости электрического поля в проекции на ось 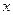 приводит к уравнению:
приводит к уравнению:
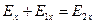 ,
,
а условие непрерывности касательных компонент векторов напряжённости электрического поля в проекции на ось 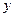 является тривиальным.
является тривиальным.
В полученные линейные алгебраические уравнения подставим уже известные зависимости и получим «магнитные» коэффициенты Френеля:
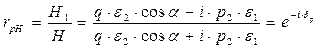
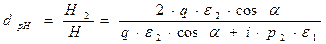 .
.
Сдвиг по фазе колебаний отражённой волны относительно падающей волны соответствует соотношению
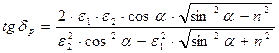 .
.
Удобнее воспользоваться выражением для половинного угла сдвига по фазе колебаний:
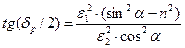 .
.
Полученные результаты, очевидно, отличаются от соответствующих выражений для случая падения на границу раздела плоской гармонической электромагнитной волны s-поляризации.
Заметим, что имеет место результат:
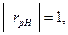
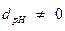 .
.
Также как и в случае падения на границу раздела двух диэлектриков 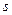 - поляризованной волны можно (принято) говорить о полном внутреннем отражении.
- поляризованной волны можно (принято) говорить о полном внутреннем отражении.
Выпишем явные выражения для комплексных амплитуд векторов напряжённости электрического поля:
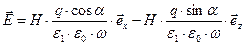 ,
, 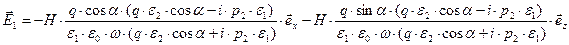 ,
,
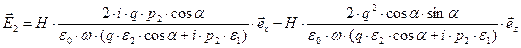 .
.
Определим формально «геометрическую длину» выписанных комплексных векторных величин по правилу 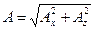 :
:
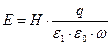 ,
,
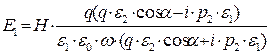 ,
,
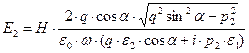 .
.
Полученные зависимости позволяют вычислить «электрические» коэффициенты Френеля:
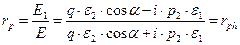 ,
,
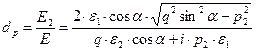 .
.
Отметим две физические закономерности. В падающей и отражённой волнах (они распространяются в одной и той же среде) отношения комплексных амплитуд напряжённости магнитного поля и напряжённости электрического поля одинаковы ( 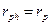 ), абсолютные значения этих комплексных величин равны единице – имеем «полное внутреннее отражение». В падающей и преломлённой волне рассматриваемые отношения не совпадают между собой – эти волны распространяются в средах с различными физическими свойствами.
), абсолютные значения этих комплексных величин равны единице – имеем «полное внутреннее отражение». В падающей и преломлённой волне рассматриваемые отношения не совпадают между собой – эти волны распространяются в средах с различными физическими свойствами.
Сравнивая между собой выражения 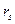 и
и 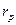 для
для 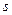 - и
- и 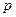 - поляризации падающей волны, убеждаемся, что они отличаются друг от друга. Это приводит к тому, что вектор напряжённости электрического поля произвольной плоско поляризованной падающей волны генерирует вектор напряжённости электрического поля отражённой волны, поляризация которого является сложной функцией точки наблюдения и момента времени.
- поляризации падающей волны, убеждаемся, что они отличаются друг от друга. Это приводит к тому, что вектор напряжённости электрического поля произвольной плоско поляризованной падающей волны генерирует вектор напряжённости электрического поля отражённой волны, поляризация которого является сложной функцией точки наблюдения и момента времени.
Продолжим изучение явления полного внутреннего отражения для случая 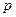 - поляризации падающей волны. Условие непрерывности нормальных компонент вектора магнитной индукции на границе раздела двух сред в рассматриваемом случае является тривиальным (по постановке задачи). Скачок нормальных составляющих векторов электрического смещения на границе раздела сред определяет величину поверхностной плотности сторонних электрических зарядов
- поляризации падающей волны. Условие непрерывности нормальных компонент вектора магнитной индукции на границе раздела двух сред в рассматриваемом случае является тривиальным (по постановке задачи). Скачок нормальных составляющих векторов электрического смещения на границе раздела сред определяет величину поверхностной плотности сторонних электрических зарядов 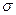 :
:
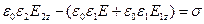 .
.
Подставляя в выписанное соотношение определённые выше зависимости, убеждаемся, что значение поверхностной плотности сторонних электрических зарядов на границе раздела двух диэлектриков равно нулю:
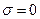 .
.
Поверхностная плотность «связанных» зарядов на поверхности раздела сред при необходимости может быть вычислена.
Таким образом, все требования классической электродинамики удовлетворены.
Вычислим действительные составляющие векторов напряжённости магнитного поля с учётом экспоненты с мнимым аргументом (бегущая волна). По аналогии с рассмотренным выше случаем 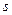 -поляризации падающей волны введём обозначение для мгновенной фазы колебаний:
-поляризации падающей волны введём обозначение для мгновенной фазы колебаний:
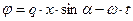 .
.
Мгновенные комплексные значения векторных полей для произвольной точки наблюдения на поверхности раздела имеют вид
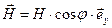 ,
, 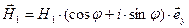 ,
, 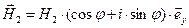 ,
,
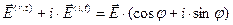 ,
, 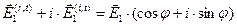 ,
,
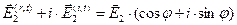 .
.
Учитывая то обстоятельство, что комплексные амплитуды электромагнитных волн действительно являются комплексными величинами, вычислим выражения для действительных значений напряжённостей электрического и магнитного полей для рассматриваемых электромагнитных волн, справедливые для произвольных моментов времени и координаты 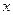 на поверхности раздела сред:
на поверхности раздела сред:
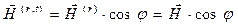 ,
, 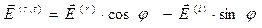 ,
,
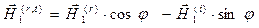 ,
, 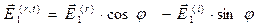 ,
,
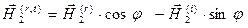 ,
, 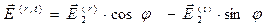 .
.
Приведём явные аналитические выражения для действительных и мнимых составляющих комплексных амплитуд рассматриваемых электромагнитных волн.
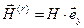 ,
, 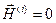 ,
,
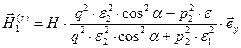 ,
, 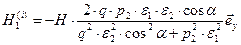
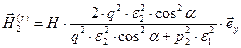 ,
, 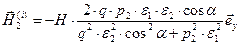 ,
,
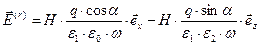 ,
, 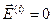 ,
, 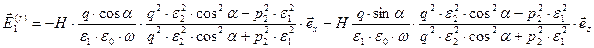 ,
, 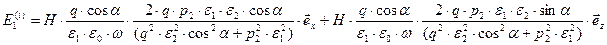 ,
,
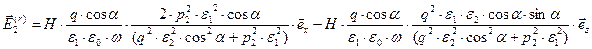 ,
,
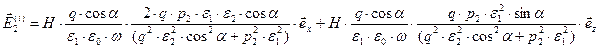 .
.
Вычислим мгновенные значения векторов Умова-Пойнтинга для падающей, отражённой и преломлённой волн:
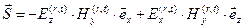 ,
,
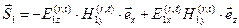 ,
,
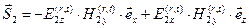 .
.
Проверим условие баланса нормальных компонент векторов Умова-Пойнтинга в произвольной точке поверхности раздела в произвольный момент времени.
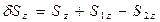 .
.
Подставляя в рассматриваемое выражение входящие в него «первичные» зависимости, определённые выше для рассматриваемого случая поляризации падающей волны, можно убедиться в справедливости утверждения:
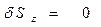 .
.
Отсюда следует, что в произвольной точке поверхности раздела диэлектрических сред в любой момент времени выполняется условие баланса плотностей потока электромагнитной энергии. Энергия электромагнитного поля не накапливается на поверхности раздела в течение произвольного промежутка времени внутри периода колебаний.
Осреднённые величины нормальных компонент векторов Умова-Пойнтинга падающей волны, отражённой волны и преломлённой волны на поверхности раздела сред, как и выше, определяются выражениями типа:
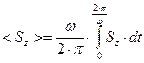 .
.
Если уравнение баланса нормальных компонент плотности потоков энергии выполняется для каждого момента времени, оно будет выполнено и для осреднённых величин:
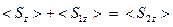 .
.
Полученный результат позволяет ввести в рассмотрение коэффициент отражения и коэффициент пропускания
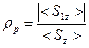 ,
, 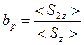 .
.
Непосредственным вычислением можно убедиться в справедливости
результатов:
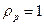 ,
, 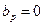 .
.
Приходим к выводу, что термин «полное внутреннее отражение» является следствием рассмотрения осреднённых нормальных составляющих векторов Умова-Пойнтига.
Вернёмся к анализу зависимостей от времени мгновенных значений нормальных компонент векторов Умова-Пойнтинга. После подстановки полученных выше результатов в интересующие нас выражения можно получить следующие зависимости:
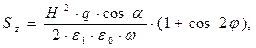
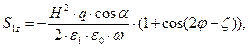
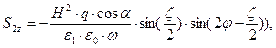
где:
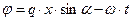 ,
, 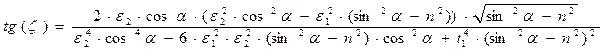 .
.
Значительно удобнее пользоваться эквивалентным соотношением
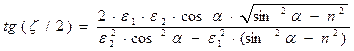 .
.
Характер зависимостей от мгновенной фазы колебаний касательных компонент векторов Умова-Пойнтинга падающей и отражённой волн продемонстрируем с помощью соотношений
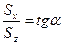 ,
, 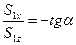 ,
,
касательную составляющую вектора Умова-Пойнтинга для преломлённой волны выпишем отдельно:
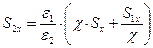 ,
, 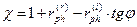 .
.
Фазы колебаний касательных компонент векторов Умова-Пойнтинга падающей и отражённой волн совпадают с фазами колебаний соответствующих нормальных компонент векторов Умова-Пойнтинга. Изменение с течением времени касательной компоненты вектора Умова-Пойнтинга преломлённой волны описывается более сложной зависимостью.
Дата добавления: 2017-09-01; просмотров: 2798;











