Уравнение плоской гармонической волны

Уравнениям (8) удовлетворяют, в частности, плоские электромагнитные гармонические волны, описываемые уравнениями

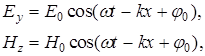(9)

где Е₀, Н₀ – амплитуды напряженностей электрического и магнитного полей; w=2p/Т=2pn – круговая частота (с^-1); Т – период колебаний (с); n=1/Т – частота колебаний (Гц); k=w/v=2p/l – волновое число; v – скорость распространения волны, для нее скорость переноса энергии (групповая скорость) u равна фазовой скорости v этой волны [см.(1.14)]; l=vT – длина волны, для вакуума

l=сT=с/n, (10)

j₀ – начальные фазы колебаний в точках с координатой x = 0.

В уравнениях гармонической волны (9) j₀ – одинаково, т.к. колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковой фазе [это следует из (1)].

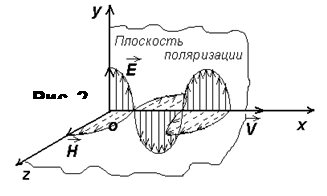
На рис.2. показаны векторы 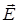и 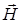поля плоской линейно поляризованной волны в различных точках луча (оси ох) в один и тот же момент времени. Плоскость, проходящая через электрический вектор 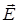и луч (или вектор ), называется плоскостью поляризации.

Электромагнитную гармоническую волну часто записывают в экспоненциальной (комплексной) форме аналогично (1.6), где вместо s и А₀ будет Е и Е₀, Н и Н₀ соответственно для электрического и магнитного векторов.

Электромагнитная волна так же, как упругая волна (см. параграф 1.3) характеризуется фронтом волны, волновой поверхностью. В отличие от упругих волн, которые распространяются только в среде (в вакууме упругие волны не могут распространяться, т.к. в нем нет частиц, которые совершали бы колебания), электромагнитные волны распространяются не только в среде, но и в вакууме, т.к. они представляют собой процесс распространения колебаний векторов 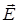и 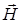в пространстве.

Как и в случае упругих волн по форме волновых поверхностей или волновому фронту различают плоские, сферические, цилиндрические и прочие электромагнитные волны.

Обычно в практике используются пучки электромагнитной энергии (света) конечного поперечного сечения. Конечный, но достаточно узкий пучок будем называть лучом. Луч всегда перпендикулярен волновому фронту.

Из уравнений Максвелла (1) следует, что электромагнитные волны являются поперечными волнами, т.к. векторы 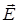и 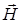колеблются перпендикулярно к направлению распространения волны (см. рис. 1 и 2).

Из (1) также следует, что

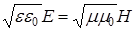, (11)