Монохроматичность и когерентность волн

3.1.1. Монохроматические волны

Монохроматическая волна – это строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Амплитуда и фаза такой волны могут изменяться от одной точки пространства к другой, частота же остается постоянной во всем пространстве.

Монохроматические волны не ограничены ни во времени, ни в пространстве, т.е. не имеют ни начала, ни конца. Поэтому они не могут быть реализованы в действительности. Однако эти идеализации играют громадную роль в учении о волнах, и мы будем ими пользоваться.

3.1.2. Расчет интерференции двух волн

Предположим, что в рассматриваемой точке наблюдения накладываются друг на друга две монохроматические световые волны, напряженности электрического поля которых [см. (2.9)]

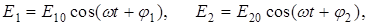(1)

частоты их одинаковы и одинаково направление колебаний вектора .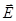

Тогда согласно принципу суперпозиции

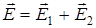(2)

или в рассматриваемом случае одинакового направления колебаний векторов 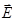₁ и 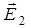Е=Е₁+Е₂ . (3)

Возводя равенство (3) в квадрат с учетом (1) и произведя усреднение по времени, получим

I=I₁+I₂+2 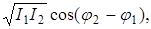(4)

где I₁и I₂ – интенсивности первой и второй волны соответственно [см. (2.20)].

Максимальная интенсивность I_макс=I₁+I₂+2 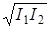будет при условии

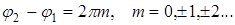, (5)

когда 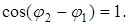При I₁=I₂=I₀ интенсивность в максимумах увеличится в 4 раза (I_макс=4I₀).

Минимальная интенсивность I_мин=I₁+I₂-2 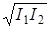будет при условии

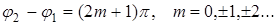, (6)

когда 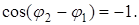При I₁=I₂=I₀ I_мин=0, т.е. свет + свет = тьма.

Следовательно, при сложении в пространстве двух (или нескольких) световых волн могут возникать в одних местах максимумы, а в других – минимумы интенсивности, т.е. светлые и темные участки, полосы.

Это явление называется интерференцией света.

Получившаяся картина будет устойчивой (т.е. она сохраняется во времени) при наложении когерентных волн, т.е. волн, излучаемых когерентными источниками.

3.1.3. Когерентные волны. Время и длина когерентности

Две волны [см. (1)] или несколько волн являются полностью когерентными (согласованными), если частоты их одинаковы, амплитуды и разность фаз постоянны, т.е.

w₁=w₂, E₁₀=const, E₂₀=const, j₂-j₁=const. (7)

Этому условию удовлетворяют монохроматические волны (1), которые неограниченны в пространстве и времени.

Из повседневного опыта известно, что при наложении света от двух независимых (некогерентных) источников излучения, например, двух электрических лампочек, никогда не удается наблюдать явление интерференции. В этом случае j₂-j₁ изменяется во времени и за время наблюдения <cos(j₂-j₁)>=0 и результирующая интенсивность I=I₁+I₂, т.е. равна сумме интенсивностей налагаемых друг на друга световых волн, а 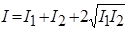не и не .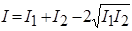

Это объясняется механизмом испускания света атомами источника излучения. В параграфе 2.4 было показано, что продолжительность процесса излучения света атомом t » 10^-8 с. За это время возбужденный атом, растратив свою избыточную энергию на излучение, возвращается в нормальное (невозбужденное) состояние и излучение им света прекращается. Затем, спустя некоторый промежуток времени, атом может вновь возбудиться и начать излучать свет.

Такое прерывистое излучение света атомами в виде отдельных кратковременных импульсов – цугов волн – характерно для любого источника света. Каждый цуг имеет ограниченную протяженность в пространстве Dx=ct и составляет 4 – 16 м в видимом диапазоне.

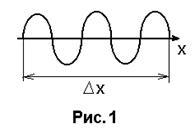Вследствие этого, а также из-за уменьшения амплитуды волны, цуг волн отличается от монохроматической волны и его можно представить в виде совокупности (суммы) монохроматических волн, круговые частоты которых лежат в интервале от w-Dw/2 до w+ Dw/2. Можно показать, что

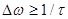. (8)

Реальная волна, излучаемая в течение ограниченного промежутка времени и охватывающая ограниченную область пространства тем более не является монохроматической. Спектр ее частот включает частоты от w-Dw/2 до w+ Dw/2.

Промежуток времени t_ког, в течение которого разность фаз колебаний, соответствующих волнам с частотами w-Dw/2 и w+Dw/2 изменяется на p, называется периодом когерентности немонохроматической волны

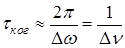. (9)

Это название связано с тем, что немонохроматическую волну можно приближенно считать когерентной с частотой w в течение промежутка времени Dt£t_ког.

Отметим, что для монохроматической волны Dw и Dn равны нулю и t_ког®¥.

Расстояние l_ког, на которое распространится волна за время когерентности, называется длиной когерентности l_ког =vt_ког. (10)

В пределах такой длины волну можно считать когерентной.

Для видимого солнечного света, имеющего спектр частот от 4×10¹⁴ до 8×10¹⁴ Гц (l=0,75 мкм и 0,375 мкм соответственно), ширина спектра Dw=2pDn=2p(8-4)×10¹⁴ =8p×10¹⁴ c^-1 и согласно (9), (10)

t_ког=2,5×10^-15 с, l_ког =0,75×10^-6 м. (11)

Заметим, что для лазеров непрерывного действия t_ког достигает 10^-2 с, а l_ког» 10⁶ м. Однако из-за неоднородности атмосферы удается наблюдать интерференцию при разности хода в несколько километров.

3.1.4. Пространственная когерентность

Наряду с временной когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности.

Одной из ее характеристик является радиус когерентности r_ког, характеризующий расстояние, на котором может быть получена четкая интерференционная картина (r_ког это не радиус окружности).

Произведение l_когr_ког²=V_ког называют объемом когерентности, в пределах которого случайная фаза волны изменяется на величину, не превосходящую p.

3.2. Методы получения когерентных волн

Для получения когерентных световых волн с помощью обычных (нелазерных) источников применяют метод разделения света от одного источника на две или нескольких систем волн (световых пучков). В каждой из них представлено излучение одних и тех же атомов источника, так что эти волны когерентны между собой и интерферируют при наложении.

Разделение света на когерентные пучки можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.

1. Метод Юнга

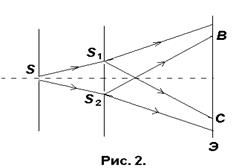
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S₁ и S₂, параллельные щели S.

Таким образом, щели S₁ и S₂играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.

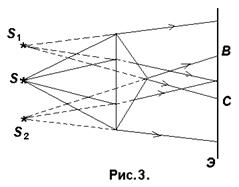
2.Бипризма Френеля.

Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.

3.3. Оптическая длина пути и разность хода

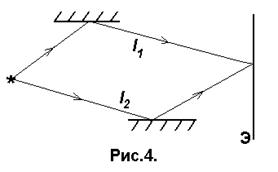
Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l₁ и l₂в средах с абсолютными показателями преломления n₁и n₂,соответственно (рис. 4). Тогда фазы этих волн [см. (1) и (2.9)] wt - j₁= wt - k₁l₁ + j₀, wt - j₂= wt - k₂l₁ + j_0, а разность фаз

j₂ -j₁ = k₂l₂ - k₁l₁= 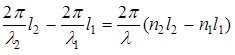, (12)

где l₁= l/n₁, l₂= l/n₂ – длины волн в средах, показатели преломления которых n₁ и n₂ соответственно, l – длина волны в вакууме.

Произведение геометрической длины пути l световой волны на абсолютный показатель преломления n называется оптической длиной пути волны.

Величину 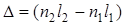(13)

называют оптической разностью хода интерферирующих волн. С учетом этого разность фаз j₂ -j₁ = 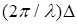. (14)

Максимальная интенсивность будет наблюдаться при j₂ -j₁ =2pm [см. (5)], когда

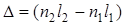=ml, 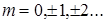, (15)

т.е. когда оптическая разность хода равна целому числу длин волн. Это условие максимума при интерференции.

Минимальная интенсивность будет наблюдаться при 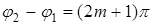[см. (6)], когда

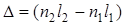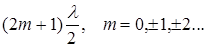= , (16)

т.е. когда оптическая разность хода равна нечетному числу полуволн (l/2). Это условие минимума при интерференции.