Фронт волны, волновые поверхности, фазовая скорость

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью(поверхностью постоянных фаз, фазовой поверхностью).

Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени – один.

Гармоническая бегущая волна (5) является плоской волной, т.к. ее волновые поверхности 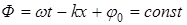представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.

Уравнение гармонической сферической волны имеет вид

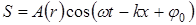, (7)

где r – радиальная координата. При распространении волны в непоглощающей среде A(r) ~ 1/r.

Скорость v распространения гармонической волны называетсяфазовой скоростью. Она равна скорости перемещения волновой поверхности. Например, в случае плоской гармонической волны из условия 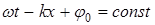следует, что

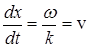. (8)

Волновое уравнение

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных.

, (9)

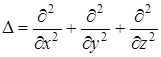где (10)

D – оператор Лапласа, v – фазовая скорость.

Решением уравнения (9) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (5), которая не зависит от координат y и z волновое уравнение принимает вид

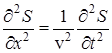. (11)

Соответствующей подстановкой можно убедится, что уравнению (11) удовлетворяет уравнение (5).