Алгебраический способ определения симметричных автоколебаний и устойчивости

Рассмотрим определение симметричных автоколеба­ний алгебраическим способом на основе гармонической линеаризации нелинейности. Пусть система (рис. 4.2) с одной нелинейностью 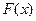имеет передаточную функцию линейной части (4.5), обладающую свойством фильтра нижних частот (раздел 4.1). Уравнения линейной части системы и нелинейного звена:

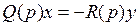
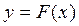
где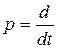

Уравнение замкнутой системы примет вид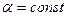

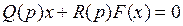(4.36)

Решение ищется приближенно в форме

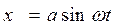(4.37)

с двумя неизвестными α и ω. После гармонической ли­неаризации (4.21) уравнение (4.35) приобретает вид

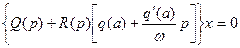(4.38)

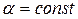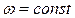Поскольку в искомом решении (4.37) и , то гармонически линеаризованное уравнение замкнутой системы (4.38) можно рассматривать как обыкновенное линейное уравнение с постоянными коэф­фициентами. Специфика его состоит лишь в том, что имеются неизвестные постоянные коэффициенты, завися­щие от искомого решения, что и позволит нам получить решение со специфическими свойствами, присущими не­линейной системе.

Запишем характеристическое уравнение гармонически линеаризованной системы:

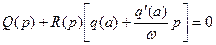(4.39)

Периодическое решение уравнения (4.38) соответ­ствует паре чисто мнимых корней 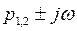характе­ристического уравнения (4.39). Поэтому для отыскания этого решения подставим в него 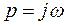. Получим

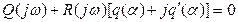
Выделим в этом выражении вещественную и мнимую части в виде

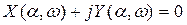
В результате получим два алгебраических уравнения

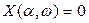
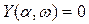(4.40)

из которых и определяются искомые амплитуда α и ча­стота ω периодического решения (4.37).

Заметим, что решение задачи упрощается в случае однозначной нелинейности F(x): вместо (4.39) здесь имеем

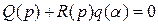
При подстановке 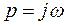выделим вещественные и мни­мые части многочленов Q и R в виде

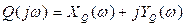
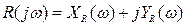
Тогда вместо (4.40) получим

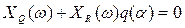
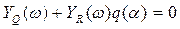
Эти два уравнения можно преобразовать к виду

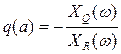
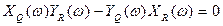(4.41)

Сначала из второго уравнения определяется частота ω периодического решения, а затем из первого уравнения определяется амплитуда α. Видно, что частота зависит от параметров линейной части и не зависит от формы однозначной нелинейности. В случае же петлевой нели­нейности это свойство нарушается и будет иметь место общий случай уравнений (4.39).

Определив таким образом периодическое решение, на­до исследовать его устойчивость. Если оно устойчиво, то это означает автоколебательный процесс. Неустойчивое периодическое решение имеет другой смысл (раздел 1.3 о неустойчивом предельном цикле).

Классический подход к исследованию устойчивости периодического решения состоит в следующем. Рассмотрим отклонение 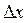от исследуемого периодического ре­шения:

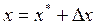
где 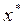вычисляется по формуле (4.15).

С учетом этого уравнение динамики системы (4.36) при­мет вид

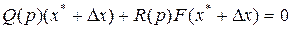
или после разложения 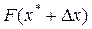в степенной ряд

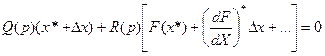
Но согласно (4.35)

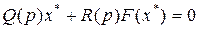
поэтому, отбросив слагаемые с производными высшего порядка, получаем уравнение в малых отклонениях

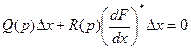
устойчивость которого надо исследовать.

Это линейное дифференциальное уравнение с перио­дическими коэффициентами. Напри­мер, если 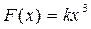, то коэффициент

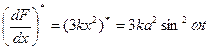
Однако исследовать точными методами устойчивость уравнения высокого порядка с периодическими коэффи­циентами весьма сложно. Поэтому обратимся к прибли­женному способу.

Дадим малые начальные отклонения 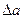амплитуды и 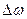частоты от их значений α и ω в периодическом решении. Тогда

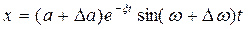(4.42)

Этим выражением описывается колебательный переход­ный процесс вблизи периодического (4.37). Для устой­чивости найденного периодического процесса необходи­мо, очевидно, чтобы в выражении (4.42) величины 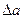и ξ имели одинаковые знаки. В этом случае при поло­жительном 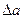амплитуда уменьшается, а при отрица­тельном 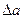— увеличивается, стремясь к значению α.

Чтобы на этом основании вывести критерий устойчи­вости, используем символическую запись выражений (4.6) и (4.42); соответственно имеем

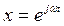
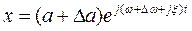
Первое решение определяется уравнением

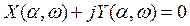
По аналогии с этим для нахождения второго решения запишем уравнение

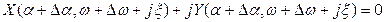
Разложив это выражение в ряд Тейлора и, использо­вав предыдущее выражение, получим

,

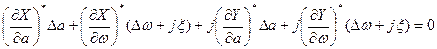где звездочка означает подстановку значений α и ω, соот­ветствующих исследуемому периодическому решению.

Если в этом выражении выделить вещественную и мнимую части, а из полученных в результате двух урав­нений исключить величину Δω, то найдем

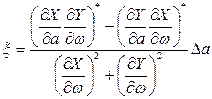
Для устойчивости периодического решения, как уже говорилось, требуется одинаковость знаков ξ и 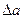. Сле­довательно, требуется, чтобы

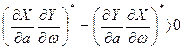(4.43)

В дополнение к этому нужно потребовать, чтобы в ха­рактеристическом уравнении гармонически линеаризован­ной системы (4.39) все остальные корни (кроме исполь­зованной нами пары чисто мнимых) имели отрицательные вещественные части, т. е. чтобы многочлен

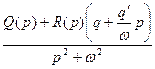(4.44)

удовлетворял критерию Гурвица (или Михайлова). В случае систем третьего и четвертого порядка для этого достаточно потребовать лишь положительности коэффи­циентов уравнения (4.38).

Итак, критерием устойчивости периодического реше­ния является неравенство (4.43) с добавлением (4.44), если исследуется система выше четвертого порядка.

Пример 4.11. Следящая система (рис. 4.13) описыва­ется уравнениями:

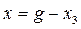
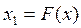
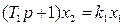
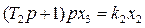
где 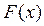— нелинейная характеристика усилителя с на­сыщением (рис. 1.5).

Уравнение линейной части при будет

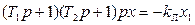
где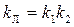

Рис.4.13. Следящая система с усилителя

с на­сыщением

Гармоническая линеаризация нелинейности, согласно (4.28), дает

k при α ≤ b

q = 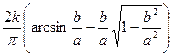при α ≥ b

Гармонически линеаризованное уравнение замкнутой си­стемы имеет вид

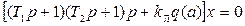(4.45)

а характеристическое уравнение —

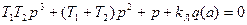
После подстановки 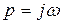получаем два уравнения

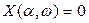
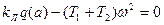
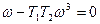(4.46)

Здесь подтверждается свойство (4.41). Из второго урав­нения определяем частоту периодического решения

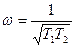(4.47)

а из первого при этом получаем

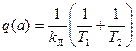(4.48)

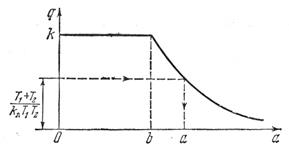
Рис.4.14. Нахождение амплитуды

периодического решения α

Используя готовый график 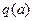(рис. 4.8, а), находим амплитуду периодического решения α, как показано на рис. 4.14.

Для определения устойчивости решения, согласно критерию (4.43), надо найти производные выражений (4.46):

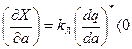
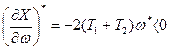
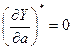
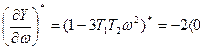
Критерий (4.43) удовлетворяется. Следовательно, имеют место автоколебания.

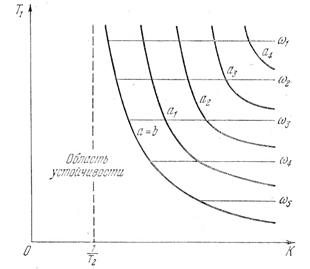
Рис. 4.15. Граница области

автоколебаний

Если учесть, что 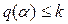(рис. 4.14), из уравнения (4.48) вытекают условия существования автоколебаний

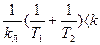
или

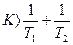(4.49)

где 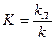— общий коэффициент усиления разомкнутой цепи данной системы в линейном плане. Легко видеть, что (4.49) представляет собой условие неустойчивости этой системы как линейной согласно критерию Гурвица. Граница устойчивости

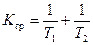
является в то же время границей области автоколебаний. Эта граница нанесена на плоскости параметров (К, Т₁) (рис. 4.15). Левее этой границы имеет место область устойчивости равновесно­го состояния системы, а правее — область автоко­лебаний, где изображены, согласно (4.47) и (4.48), линии равных значений α и ω.

Зависимость амплиту­ды автоколебаний от ко­эффициента К изображе­на на рис. 4.16.

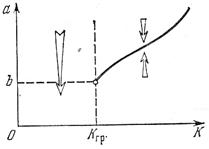
Рис. 4.16. Зависимость

амплиту­ды

автоколебаний от К

Если ве­личину α трактовать ши­ре — как амплитуду колебаний в переходном процессе, то стрелками (рис. 4.16) можно показать направление изменения амплитуды в разных областях значений К. В линейной системе (без насыщения) при 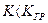было бы затухание, а при 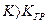— неограниченно расходящиеся колебания. В не­линейной системе (с насыщением) колебания при 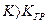расходятся не до бесконечности, а до определен­ной амплитуды. При больших же начальных отклонени­ях они даже затухают (рис. 4.16), так как имеется устой­чивый автоколебательный режим.

Пример 4.12. Пусть теперь в той же следящей си­стеме (рис. 4.13) усилитель имеет релейную характе­ристику (рис. 1.3). Уравнение замкнутой системы имеет вид (4.45), где, в отличие от прежнего случая,

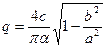при α ≥ b

Решения (4.47) и (4.48) сохраняют свой вид. Меня­ется только график q(α). Подобно рис. 4.6, б он показан здесь на рис. 4.17.

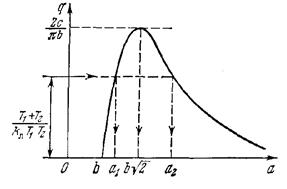
Рис.4.17. График q(α)

Уравнение (4.48) имеет два реше­ния α₁ и α₂ (рис. 4.17), причем в точках α₁ и α₂ имеем соответственно 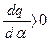и 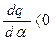. С учетом этого знаки производных в критерии устойчивости периодиче­ского решения (4.43) оказываются такими, что в точке α₁ критерий не выполняется (решение неустойчиво), а в точке α₂ — выполняется. В соответствии с этим реше­нием (рис. 4.17) на рис. 4.18 изображена зависимость амплитуды автоколебаний (α₂) и амплитуды неустойчи­вого периодического решения (α₁) в зависимости от коэффициента усиления линейной части системы 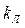. Стрел­ками обозначены направления изменения амплитуды ко­лебаний в переходных процессах. Величина 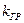(рис. 4.18) соответствует точке максимума на рис. 4.17, т. е.

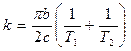
При 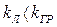равновесное состояние устойчиво при любых начальных условиях. Если 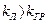, то равновес­ное состояние устойчиво лишь при малых начальных от­клонениях (ниже линии α₁), а при больших начальных отклонениях (выше линии α₁) устанавливаются автоко­лебания с амплитудой α₂.

Здесь имеет место пример присущей нелинейным си­стемам существенной зависимости характера поведения системы от порядка величин начальных условий. Линии α₁ и α₂ (рис. 4.18) разделяют области притяжения раз­личных установившихся режимов по начальным ус­ловиям.

На рис. 4.19 показан результат решения той же за­дачи при идеальном реле, а на рис. 4.20 — при петлевой характеристике реле. Последний случай отличается тем, что характеристическое уравнение вместо прежнего

Рис.4.18. Зависимость амплитуд Рис.4.19. Результат

(α₁) и (α₂) от k_Л решения за­дачи при

идеальном реле

по­лучает вид

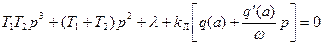
где, согласно (4.23),

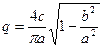
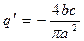
После подстановки 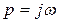получаем

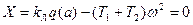
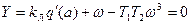(4.50)

Исключив k_Л из этих уравнений, с подстановкой выра­жения q'(α) получим

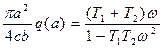
откуда определяется ω(α) при заданных Т₁ и Т₂. После этого из второго уравнения (4.50) имеем

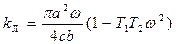
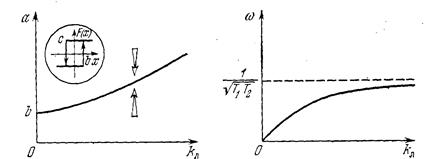
а) б)

Рис.4.20. Зависимости α(k_Л) и ω(k_Л)

Это позволяет, с учетом полученной выше зависимости ω(α), по­строить зависимости α(k_Л) и ω(k_Л), изображенные на рис. 4.20. Решение характеризуется наличием зави­симости ω(k_Л) (рис. 4.20, б) в отличие от всех преды­дущих примеров, где частота ω (4.47) не зависела от К и .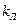

Заметим, что в отличие от случаев, показанных на рис. 4.19 и 4.20, с мягким возбуждением автоколебаний при любых параметрах системы, на рис. 4.18 для релей­ной системы с зоной нечувствительности имеем область устойчивости равновесного состояния ( 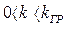) и жесткое возбуждение автоколебаний при 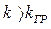(тре­бующее заброса начального состояния системы за ли­нию α₁, т. е. α₀ > α₁).