Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Линейное однородное дифференциальное уравнение второго порядка c постоянными коэффициентами – это уравнение y′′ + py′ + qy = 0 (7), где p и q – постоянные величины.

Общее решение дифференциального уравнения второго порядка имеет вид y = φ(x; c₁, c₂), где c₁, c₂ - некие постоянные величины.

Частное решение y = φ(x; c₁₀, c₂₀) получается из общего решения при выполнении начальных условий , .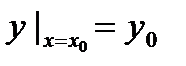

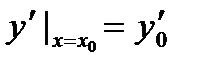Общее решение уравнения (7) зависит от решений характеристического уравнения

k² + pk + q = 0.

Характеристическое уравнение получается из дифференциального уравнения (7) подстановкой функции .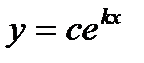

1) Если корни k₁ и k₂ характеристического уравнения действительные и различные, то

.

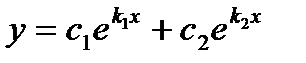2) Если корни k₁ и k₂ характеристического уравнения действительные и равные, то

.

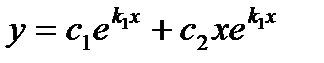3) Если корни k₁ и k₂ характеристического уравнения комплексные (k₁ = α + βi, k₂ = α – βi), то

.

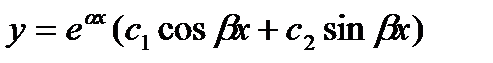@ Задача 1. Найти общее решение дифференциального уравнения: y′′ – 2y′ + y = 0.

Решение: Корни k₁ и k₂ характеристического уравнения k² – 2k + 1 = 0 действительные и равны 1. Общее решение дифференциального уравнения имеет вид:

.

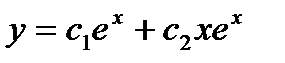Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами

Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами – это уравнение 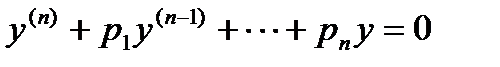, где p₁, p₂, …, p_n – постоянные величины.

1) Если все корни характеристического уравнения действительные и различные, то общее решение имеет вид

.

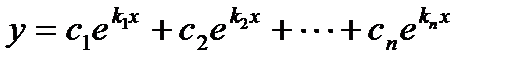2) Если все корни характеристического уравнения действительные, но не все различные (с кратностью m), то общее решение содержит частные решения , , … .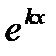

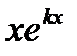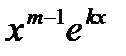3) Если какая-либо пара сопряженных комплексных корней имеет кратность m, то решение содержит частные решения 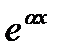cosbx, x 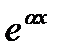cosbx, … ,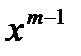 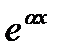cosbx, 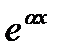sinbx, x 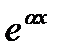sinbx, … ,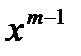 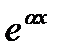sinbx.

@ Задача 2. Найти общее решение дифференциального уравнения: .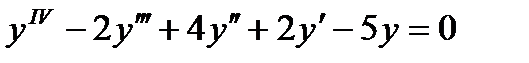

Решение: Корни характеристического уравнения 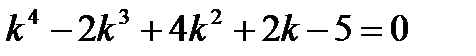равны – 1; 1; 1 + 2i и 1 – 2i. Общее решение дифференциального уравнения имеет вид:

.