Линейное дифференциальное уравнение. Дифференциальное уравнение Бернулли

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде y′ + p(x)y = g(x) (5), где p(x) и g(x) – заданные функции.

Особенность линейного дифференциального уравнения в том, что функция y и ее производная y′ входят в уравнение в первой степени, не перемножаясь между собой.

Линейное дифференциальное уравнение первого порядка решается методом Лагранжа (методом вариации произвольной постоянной). Рассматривается линейное однородное дифференциальное уравнение без правой части y′ + p(x)y = 0, решение которого имеет вид 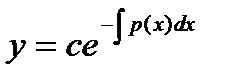. После этого постоянная с заменяется функцией c(x) и, решение однородного уравнения подставляя в неоднородное уравнение (5), получается уравнение для функции c(x):

,

.

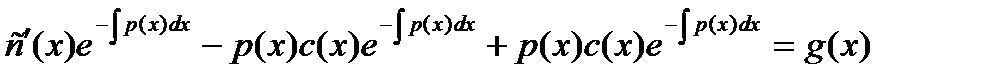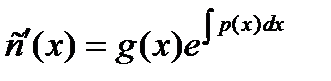В итоге, общее решение уравнения (5) имеет вид

.

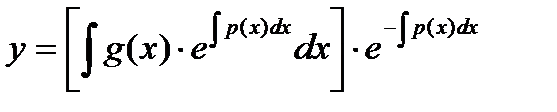@ Задача 4. Найти общее решение дифференциального уравнения: y′ + 2xy = 2x.

Решение: Подставим p(x) = 2x и g(x) = 2x в общее решение линейного дифференциального уравнения:

.

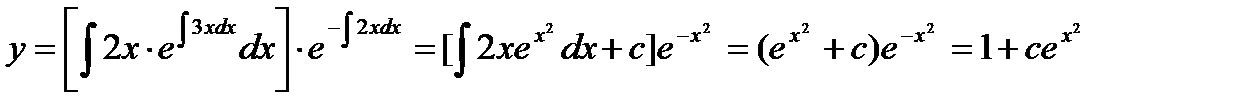Уравнение вида 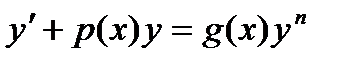при n ¹ 0; 1 называется уравнением Бернулли.