Интегральный признак Коши

Теорема: Если каждый член положительного ряда меньше предшествующего, то: а) если предел 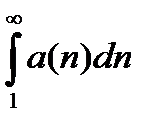конечный, то ряд (1) сходится, б) если предел бесконечный, то ряд (1) расходится.

@ Задача 5. Исследовать на сходимость гармонический ряд .

Решение: Из интегрального признака Коши 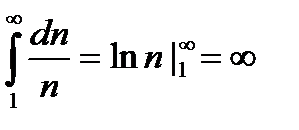следует, что ряд расходится.

Ряд называется знакопеременным, если его члены поочередно положительны и отрицательны. Достаточным признаком сходимости знакопеременного числового ряда являются признак Лейбница.

Признак Лейбница

Знакопеременный ряд сходится, если его члены стремятся к нулю, все время убывая по абсолютному значению.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· сходится согласно признаку Лейбница.

Знакопеременный ряд называется абсолютно сходящимся, если сходится положительный ряд, составленный из абсолютных значений членов данного ряда.

! Пример: Знакопеременный ряд 1 – 1/4 + 1/9 – 1/16 + ··· является абсолютно сходящимся.

Знакопеременный рядможет сходиться и тогда, когда ряд, составленный из абсолютных значений его членов, расходится.

Знакопеременный ряд называется условно сходящимся, если он сходится, но ряд, составленный из абсолютных значений его членов, расходится.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· является условно сходящимся.

СТЕПЕННЫЕ РЯДЫ