Дифференциальное уравнение в полных дифференциалах

Уравнение P(x; y)dx + Q(x; y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x; y), что имеет место при выполнении условия 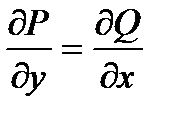. (6)

Если левая часть дифференциального уравнения представить в виде полного дифференциала, то получим 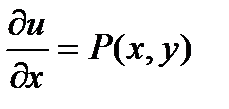, 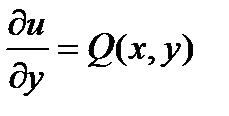. Интегрируем первое уравнение: 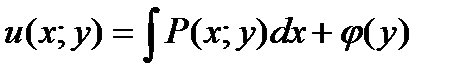. Применяя второе уравнения, получим уравнение для неизвестной j(y): 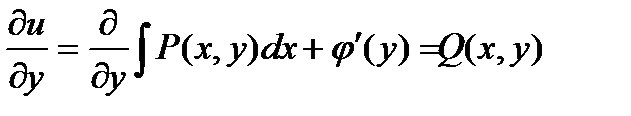, откуда можно найти j(y):

.

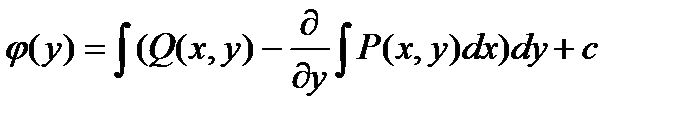В итоге общее решение дифференциального уравнения в полных дифференциалах имеет вид

.

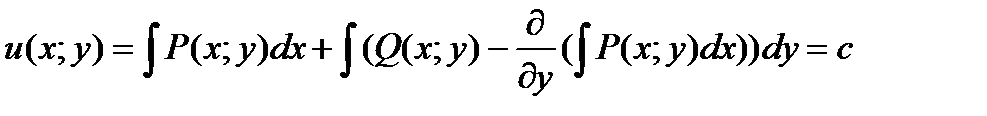@ Задача 5. Найти общее решение дифференциального уравнения (2xy – 5)dx + (3y² + x²)dy = 0.

Решение: Проверим выполнение условия (6): 2x = 2x. Подставим P(x; y) = 2xy – 5 и Q(x; y) = 3y² + x² в общее решение дифференциального уравнения в полных дифференциалах: =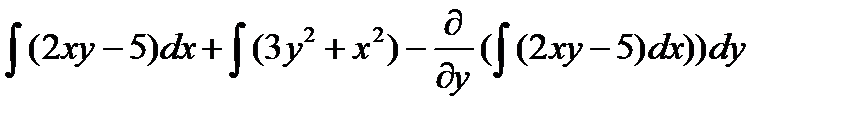

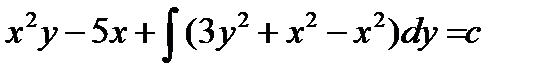= , x²y – 5x + y³ = c.

Правило: Чтобы найти общее решение дифференциального уравнения, интегрируем 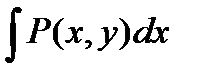при постоянном значении y, интегрируем 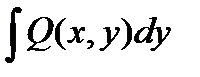при постоянном x и объединяем эти выражения, сохраняя повторяющие члены только один раз.

Линейные дифференциальные уравнения с постоянными коэффициентами