Признак сравнения рядов

Сходимость такого ряда устанавливается путем сравнения его с другим (эталонным) рядом.

Если ряд 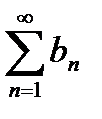, общие члены которого 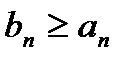, сходится, то сходится также ряд (1).

Если ряд 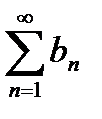, общие члены которого 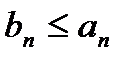, расходится, то расходится также ряд (1).

@ Задача 2. Исследовать на сходимость числовой ряд .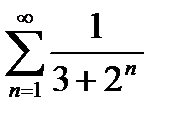

Решение: По признаку сравнения рядов, так как ряд 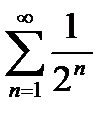сходится, а также выполняется условие 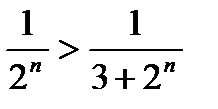, следовательно, наш ряд тоже сходится.

@ Задача 3. Исследовать на сходимость числовой ряд .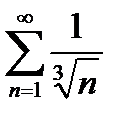

Решение: Согласно признаку сравнения т.к. 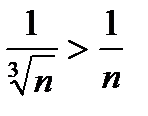, и гармонический ряд расходится, то приведенный ряд также расходится.

Признак Даламбера

Ряд сходится, если .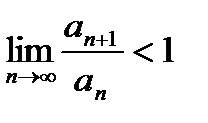

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Даламбера целесообразно применить, когда общий член ряда содержит выражение вида n! или .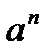

@ Задача 3. Исследовать на сходимость ряд .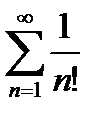

Решение: По признаку Даламбера 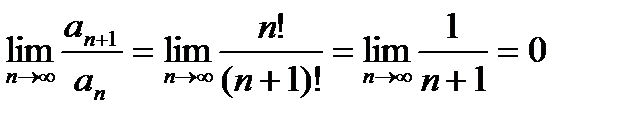, т.е. ряд сходится.

Признак Коши

Ряд сходится, если .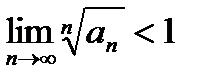

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Коши целесообразно применить, когда общий член ряда содержит выражение вида .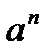

@ Задача 4. Исследовать на сходимость ряд .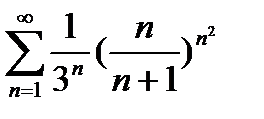

Решение: По признаку Коши 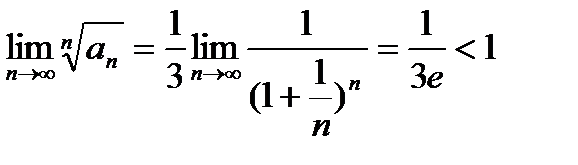, т.е. ряд сходится.