Достаточное условие экстремума

Обозначим через .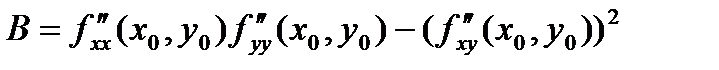

1. Если 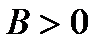, , 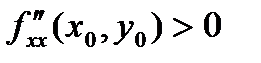, 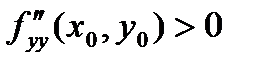то функция в точке экстремума имеет минимум.

2. Если 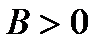, , 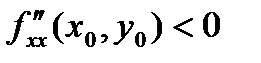, 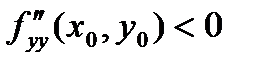то функция в точке экстремума имеет максимум.

3. Если 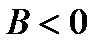, то функция не имеет ни минимума, ни максимума.

4. Если B = 0, то функция может иметь экстремум или не иметь. Нужны дополнительные исследования, чтобы ответить на этот вопрос.

Разыскание максимума или минимума в критической точке можно осуществить и с помощью определения максимума и минимума. Для этого необходимо найти значение функции в критической точке и вблизи этой точки.

@ Задача 1. Найти координаты экстремальных значений функции .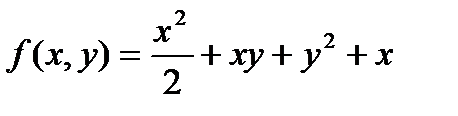

Решение: Из необходимого условия экстремума находится критическая точка (точка экстремума): f¢_x= x + y + 1= 0, f¢_y= x + 2y = 0, x₀ = – 2, y₀ = 1.

С помощью достаточного условия экстремума находятся минимум или максимум функции: 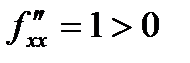, , 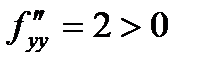, 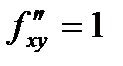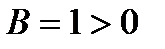. Функция в точке экстремума имеет минимум: f_min(– 2, 1) = – 1.

@ Задача 2. Небольшая фирма производит два типа товара A и B и продает их по цене 1000 и 800 рублей, соответственно. Функция издержек (затрат) имеет вид C = 2Q₁² + 2Q₁Q₂ + Q₂², где Q₁и Q₂ - объемы выпуска товаров A и B. Для каких значений Q₁и Q₂ прибыль фирмы будет максимальной (задача оптимизации)?

Решение: Прибыль определяется как

П = R – C = 1000Q₁ + 800Q₂ – 2Q₁² – 2Q₁Q₂ – Q₂². Из необходимого условия экстремума находим Q₁= 100, Q₂ = 300. П_max = П(100, 300) = 170000.

<5 6 789 10 11 >

Дата добавления: 2016-06-15; просмотров: 1460;