Дифференциальное уравнение первого порядка
Дифференциальное уравнение первого порядка – это уравнение, связывающее независимую переменную x, искомую функцию y и ее первую производную y′:
F(x; y; y′) = 0. (1)
Пример: xy′ + ylny′ = 0.
Если уравнение (1) разрешается относительно y′, то его записывают в виде y′ = f(x; y) (2) и оно называется дифференциальным уравнением первого порядка, разрешенным относительно производной y′.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: P(x; y)dx + Q(x; y)dy = 0. (3)
Уравнение вида (2) сводится к уравнению дифференциальной формы (3) следующим образом:
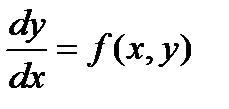 , dy = f(x; y)dx, f(x; y)dx – dy = 0.
, dy = f(x; y)dx, f(x; y)dx – dy = 0.
Обратный переход из (3) в (2) производится делением уравнения (3) на dx: 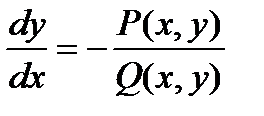 .
.
Общим решением дифференциального уравнения первого порядка называется функция y = φ(x; c), которая является решением уравнения при каждом фиксированном значении постоянной с.
Частным решением дифференциального уравнения первого порядка называется функция y = φ(x; c0), удовлетворяющая начальному условию 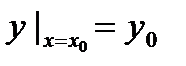 . (4)
. (4)
В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Задача нахождения частного решения дифференциального уравнения называется задачей Коши.
Теорема существования и единственности решения задачи Коши: Если в уравнении (2) функция f(x; y) и ее частная производная f¢y(x, y) непрерывны в некоторой области D, содержащей точку (x0, y0), то существует единственное решение y = φ(x; c0) этого уравнения, удовлетворяющее начальному условию (4).
Пример: Решениями дифференциального уравнения y′ = 3x2 являются y = x3, y = x3 + 1, y = x3 + 3и т.д. Другими словами, общее решение дифференциального уравнения представляет собой семейство интегральных кривых y = x3 + c. Из этого множества функций есть только одна, график которой проходит через заданную точку, т.е. удовлетворяет начальному условию (4). В частности, при 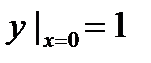 решение дифференциального уравнения имеет вид y = x3 + 1.
решение дифференциального уравнения имеет вид y = x3 + 1.
Из дифференциального уравнения (2) следует, что угловой коэффициент касательной к интегральной кривой в каждой ее точке равен правой части этого уравнения, т.е. функции f(x; y). Если построить семейство функций f(x; y) = c (изоклины), то для каждого c во всех точках функции f(x; y) = c производная y′ постоянная, т.е. угловые коэффициенты одинаковые. Если в каждой точке построить эти касательные, то получим поле направлений данного уравнения. В этом и заключается геометрический смысл дифференциального уравнения первого порядка. Задача интегрирования уравнения (2) геометрически формулируется так: найти линии, у которых направление касательной всюду совпадает с направлением поля.
Дата добавления: 2016-06-15; просмотров: 2186;











