Понятие конечных разностей
Пусть на сетке 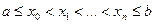 для
для 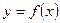 заданы значения
заданы значения 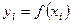 для равноотстоящих значений независимой переменной:
для равноотстоящих значений независимой переменной: 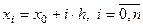 , где h − шаг интерполяции. Точки
, где h − шаг интерполяции. Точки 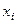 называются узлами интерполяции.
называются узлами интерполяции.
Введем понятие конечных разностей. В математической литературе используется три типа конечных разностей: 1) нисходящие разности 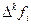 для интерполяции вперед, 2) восходящие разности
для интерполяции вперед, 2) восходящие разности 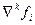 для интерполяции назад, 3) центральные разности
для интерполяции назад, 3) центральные разности  для построения центральных интерполяционных формул.
для построения центральных интерполяционных формул.
Пусть известны значения функции в узлах 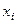 :
: 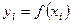 . Составим разности значений функции.
. Составим разности значений функции.
Конечной разностью первого порядка называется разность между значениями функции в данном узле и в предыдущем:
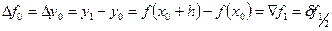
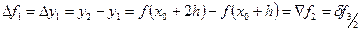 ,
,
…………………………………………….
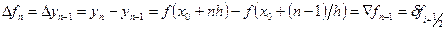 .
.
Это определение можно записать в другой форме:
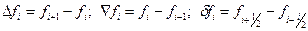
Можно составить вторые разности функции:
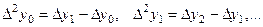 ,
,
Иначе 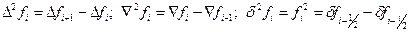
Аналогично составляются конечные разности порядка k:
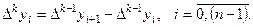
При помощи конечных разностей были построены интерполяционные многочлены: 1) многочлен Стирлинга, который используется при построении многочлена четной степени и строится по нечетному числу узлов, 2) многочлен Бесселя, который используется при построении многочлена нечетной степени и строится по четному числу узлов, 3) первый и второй интерполяционные многочлены Ньютона, когда точка интерполирования находится в начале или в конце таблицы.
Оценка погрешности замены функции многочленами Pn(x):
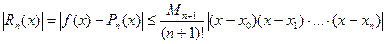 , где
, где 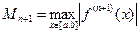 .
.
Дата добавления: 2016-06-15; просмотров: 4074;











