Метод прямоугольников
Метод прямоугольников является наиболее простым методом приближенного вычисления интеграла. Он основан на непосредственном определении определенного интеграла:
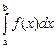 =
= 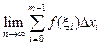 ,
,
где 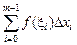 – интегральная сумма, соответствующая некоторому произвольному разбиению отрезка [a; b] на m частей и некоторому выбору точек x0, x1 , ... ,xm – 1 на отрезках разбиения.
– интегральная сумма, соответствующая некоторому произвольному разбиению отрезка [a; b] на m частей и некоторому выбору точек x0, x1 , ... ,xm – 1 на отрезках разбиения.
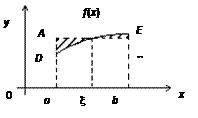 |
Вычисление определенного интеграла I = 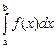 геометрически сводится к вычислению площади криволинейной трапеции, ограниченной функцией f(x) и прямыми х = а, х = b.
геометрически сводится к вычислению площади криволинейной трапеции, ограниченной функцией f(x) и прямыми х = а, х = b.
Заменим криволинейную трапецию DЕba прямоугольником АВba, проведя АВ так, чтобы фигуры DAC и CEB получились примерно равными. Тогда площади криволинейной трапеции и прямоугольника АВba будут примерно равны. Учитывая, что высота прямоугольника равна f(x), а основание (b – a), можно записать: f(x)dx » (b – a) f(x).
Для увеличения точности численного интегрирования можно отрезок [a; b] разбить на несколько частей и для каждой из них вычислить приближенное значение площади криволинейной трапеции, основанием которой является отрезок Δxi = xi+1 – xi (i = 0, ..., m–1), а высотой число f(xi), где xi Î [xi, xi+1], тогда
f(x)dx » f(x0) Δx0 + f(x1) Δx1 + ... + f(xn–1) Δxm–1 .
Практически удобно делить [a; b] на равные части, а точки xi совмещать с левыми (f(xi)=f(xi)) или правыми (f(xi)=f(xi+1)) концами отрезков разбиения.
Тогда приближенное значение интеграла геометрически равно площади заштрихованной ступенчатой фигуры и может быть представлено:
1) формулой левых прямоугольников (рис. 1):
I = 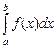 =
= 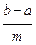 (у0+ у1+...+ уm-1) = h
(у0+ у1+...+ уm-1) = h 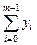 , где h =
, где h = 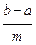 , (1)
, (1)
2) формулой правых прямоугольников (рис. 2):
I = 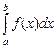 =
= 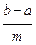 (у1 + ... + уm) = h
(у1 + ... + уm) = h 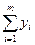 . (2)
. (2)
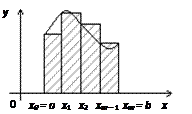
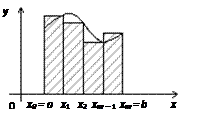
Рис. 1 Рис. 2
Оценка погрешности: 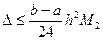 , где
, где 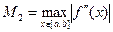
Формулы прямоугольников – это простейшие квадратурные формулы. Существуют квадратурные формулы Ньютона -_Котеса, частными случаями которых являются формула трапеций, формула Симпсона или парабол.
Метод трапеций
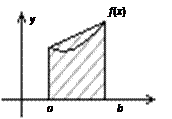 Приближенное значение определенного интеграла можно найти, заменив на отрезке [а; b] дугу АВ графика подынтегральной функции у = f(x) стягивающей ее хордой и вычисляя площадь трапеции АВba.
Приближенное значение определенного интеграла можно найти, заменив на отрезке [а; b] дугу АВ графика подынтегральной функции у = f(x) стягивающей ее хордой и вычисляя площадь трапеции АВba.
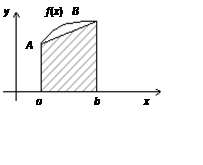 |
Рис. 3 Рис. 4
Примем значение определенного интеграла численно равным площади этой трапеции:
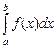 » (b – a)
» (b – a) 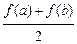 – формула трапеций.
– формула трапеций.
Если f/ //(x) > 0, то вычисления по формуле трапеций дает значение интеграла с избытком (рис. 3); если f //(x) < 0, то интеграл вычисляется с недостатком (рис. 4).
Для простоты вычислений удобно делить [a; b] на равные части (m частей). Длина каждого из отрезков разбиения Dxi = 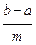 , тогда для отрезка [ xi; xi+1]
, тогда для отрезка [ xi; xi+1]
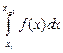 »
» 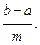
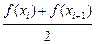 ,
,
а на всем отрезке [a; b] численное значение интеграла равно 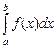 »
» 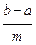
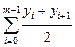 ,
,
или, так как уi под знаком å встречается дважды, 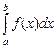 »
» 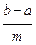
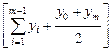 .
.
Перепишем данное выражение в более удобном виде:
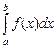 »
» 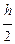 (у0 + 2у1 + 2у2 + ... + 2уm-1 + уm), где h =
(у0 + 2у1 + 2у2 + ... + 2уm-1 + уm), где h = 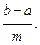 (3)
(3)
Получили формулу трапеций для приближенного вычисления определенного интеграла.
Оценка погрешности: 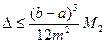 , где
, где 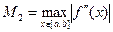 .
.
Пример. Вычислить интеграл 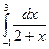 по формулам прямоугольников и трапеций. Оценить погрешность.
по формулам прямоугольников и трапеций. Оценить погрешность.
Решение.
Разобьем отрезок интегрирования [-1; 3] на 4 равные части. Рассмотрим подынтегральную функцию 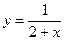 и составим таблицу ее значений с шагом h = 1:
и составим таблицу ее значений с шагом h = 1: 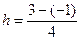 .
.
| х | -1 | ||||
| у | 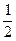
| 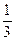
| 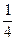
| 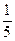
|
1) Метод прямоугольников.
Вычислим интеграл, пользуясь формулой левых прямоугольников (1):
I = 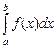 =h (у0+ у1+...+ уm-1), тогда
=h (у0+ у1+...+ уm-1), тогда 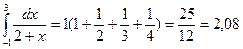 .
.
Вычислим интеграл, пользуясь формулой правых прямоугольников (2):
I = 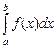 =h (у1+...+ уm), тогда
=h (у1+...+ уm), тогда 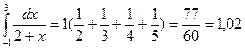 .
.
В данном примере легко посчитать точное значение интеграла: 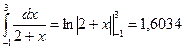 , следовательно, по формуле левых прямоугольников значение нашли с избытком, по формуле правых – с недостатком.
, следовательно, по формуле левых прямоугольников значение нашли с избытком, по формуле правых – с недостатком.
Для оценки погрешности этого найдем производные подынтегральной функции:
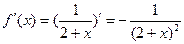 ,
, 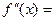
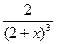 .
.
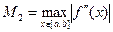 =
= 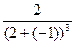 = 2, тогда погрешность
= 2, тогда погрешность 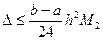 =
= 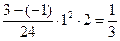 .
.
2) Метод трапеций.
Формула трапеций (3): 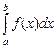 »
» 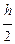 (у0 + 2у1 + 2у2 + ... + 2уm-1 + уm),
(у0 + 2у1 + 2у2 + ... + 2уm-1 + уm),
тогда 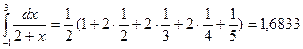
Найдем погрешность. 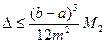 =
= 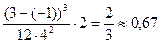 .
.
Дата добавления: 2016-06-15; просмотров: 4966;











