П. 3. Интерполирование

Интерполяция – частный случай аппроксимации.

Определение. Процесс вычисления значений аппроксимирующей функции j(x) в точках x, отличных от заданных в таблице, называется интерполированием функции f(x).

Математическая постановка задачи интерполирования для функции одной переменной:

пусть на отрезке 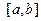задана функция 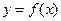своими (n + 1) значениями: 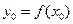, ,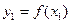…, 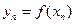в точках x₀ , x₁, …, x_n , то есть задана в виде таблицы:

Требуется построить аппроксимирующую функцию φ(x), совпадающую в узлах х_i со значениями заданной функции 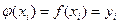. Функция φ(x) называется интерполяционной, точки х_i – узлами интерполяции.

Интерполяция - это вид точечной аппроксимации.

Геометрически задача интерполирования для функции одной переменной 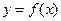означает построение на плоскости кривой проходящей через точки с координатами (x₀, у₀), (x₁, у₁), …, (x_n, у_n).

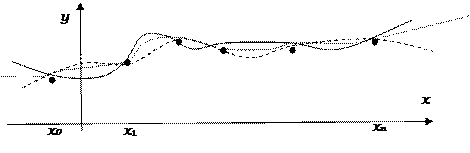
Из рисунка интуитивно видно, что через данные точки можно провести бесчисленное множество различных кривых. Задача становится однозначной, если в качестве интерполирующей функции выбрать, например, многочлен.

Определение. Если аргумент х, для которого определяется приближенное значение функции, принадлежит отрезку [x₀, x_n], то задача определения значения функции в точке х называется интерполированием в узком смысле. Если же аргумент х находится вне отрезка [x₀, x_n], то поставленная задача называется экстраполированием.

Определение.Если на заданном отрезке [x₀, x_n] для функции 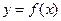строится несколько аппроксимирующих функций, отдельно на каждой части данного отрезка, то такая интерполяция называется локальной (линейная, квадратичная). Глобальная интерполяция –построение интерполяционного многочлена, единого для всего отрезка[x₀, x_n], график такого многочлена должен проходить через все заданные в таблице точки.Пример - многочлен Лагранжа.