П.1. Постановка задачи Коши
Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид:
y' (x) = f(x, y(x)).
Решением уравнения является дифференцируемая функция y(x), которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой.
Производную y'(x) в каждой точке (x, y) можно геометрически интерпретировать как тангенс угла 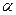 наклона касательной к графику решения, проходящего через эту точку, т е.
наклона касательной к графику решения, проходящего через эту точку, т е.
k = tg 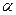 = f (x, y).
= f (x, y).
Уравнение y' (x) = f(x, y(x)) определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: y ( 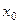 ) =
) = 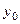 , где
, где 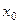 – начальное значение аргумента x, а
– начальное значение аргумента x, а 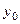 – начальное значение функции.
– начальное значение функции.
Задача Коши заключается в отыскании функции y = y(x), удовлетворяющей уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения 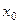 , т. е. для
, т. е. для 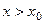 .
.
Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения y(x) на некоторой выбранной сетке значений аргумента 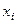 , i = 0, 1, …n. Точки
, i = 0, 1, …n. Точки 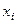 называются узлами сетки, а величина
называются узлами сетки, а величина 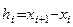 – шагом сетки. Часто рассматривают равномерные сетки, для которых шаг
– шагом сетки. Часто рассматривают равномерные сетки, для которых шаг 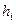 постоянен,
постоянен, 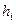 = h =
= h = 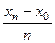 . При этом решение получается в виде таблицы, в которой каждому узлу сетки
. При этом решение получается в виде таблицы, в которой каждому узлу сетки 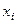 соответствуют приближенные значения функции y(x) в узлах сетки
соответствуют приближенные значения функции y(x) в узлах сетки 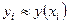 .
.
Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений.
Сходимость численных методов решения задачи Коши.
Пусть y(x) – решение задачи Коши. Назовем глобальной погрешностью (или просто погрешностью) численного метода функцию 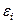 =
= 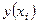 –
– 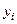 , заданную в узлах сетки
, заданную в узлах сетки 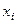 . В качестве абсолютной погрешности примем величину R =
. В качестве абсолютной погрешности примем величину R = 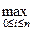 | y
| y 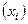 –
– 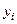 |.
|.
Численный метод решения задачи Коши называется сходящимся, если для него R→0 при h→0. Говорят, что метод имеет p-ый порядок точности, если для погрешности справедлива оценка R ≤ C 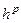 , p > 0, C – константа, C ≠ 0.
, p > 0, C – константа, C ≠ 0.
П.2. Метод Эйлера
Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши
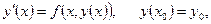
на отрезке 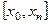 . Выберем шаг
. Выберем шаг 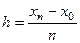 и построим сетку с системой узлов
и построим сетку с системой узлов 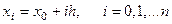 , вычислим приближенные значения функции y(x) в узлах сетки
, вычислим приближенные значения функции y(x) в узлах сетки 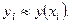 Заменив производную y' (x) конечными разностями на отрезках [
Заменив производную y' (x) конечными разностями на отрезках [ 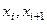 ], i = 0, 1, …, n -1, получим приближенное равенство
], i = 0, 1, …, n -1, получим приближенное равенство 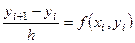 , i = 0, 1, …, n -1, которое можно переписать так:
, i = 0, 1, …, n -1, которое можно переписать так:
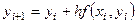 , i = 0, 1, …, n - 1.
, i = 0, 1, …, n - 1.
Данные формулы и начальное условие являются расчетными формулами метода Эйлера.
Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке [ 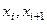 ] заменяется касательной
] заменяется касательной
y - 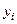 = y' (
= y' ( 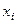 )( x –
)( x – 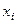 ),
),
проведенной в точке ( 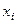 , y(
, y( 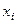 )) к интегральной кривой, проходящей через эту точку. После выполнения n шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера).
)) к интегральной кривой, проходящей через эту точку. После выполнения n шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера).
Оценка погрешности. Для оценки погрешности используется правило Рунге, которое заключается в следующем. Пусть 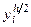 - приближения, полученные с шагом
- приближения, полученные с шагом 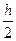 , а
, а 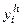 - приближения, полученные с шагом h. Тогда справедливо приближенное равенство:
- приближения, полученные с шагом h. Тогда справедливо приближенное равенство:
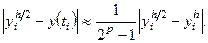
Таким образом, чтобы оценить погрешность одношагового метода с шагом h, нужно найти то же решение с шагом h и вычислить величину, стоящую справа в формуле, т. е.
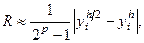
где p – порядок точности. Так как метод Эйлера имеет первый порядок точности, т. е. p = 1, то приближенное равенство примет вид: 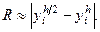
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью 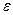 . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение
. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение 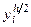 , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие: 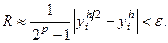 Для метода Эйлера это условие имеет вид:
Для метода Эйлера это условие имеет вид: 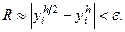 Приближенным решением будут значения
Приближенным решением будут значения 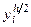 , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример.
Найдем решение на отрезке 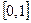 следующей задачи Коши:
следующей задачи Коши: 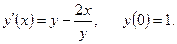
Решение.
Возьмем шаг h = 0.2. Тогда 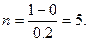
В соответствии с формулами получим расчетную формулу Эйлера:
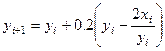 ,
, 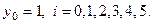
Решение представим в виде таблицы:
| i | ||||||
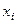
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
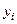
| 1.0000 | 1.2000 | 1.3733 | 1.5294 | 1.6786 | 1.8237 |
Исходное уравнение есть уравнение Бернулли. Его решение можно найти в явном виде:
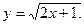
Для сравнения точного и приближенного решения представим точное решение в виде таблицы:
| i | ||||||
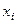
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
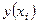
| 1.0000 | 1.1832 | 1.3416 | 1.4832 | 1.6124 | 1.7320 |
Из таблицы видно, что погрешность составляет:
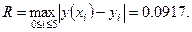
Дата добавления: 2016-06-15; просмотров: 3700;











