Квадратичная интерполяция

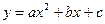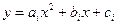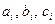Если интерполирующая функция - многочлен второго порядка , то интерполяция называется квадратичной. Иногда ее называют параболической на отрезке [x_i-1, x_i+1], так как квадратный трехчлен - это парабола , где - неизвестные. Для их определения необходимо условие прохождения параболы через три точки: .

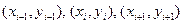Эти условия запишем в виде:

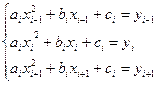
Решив систему, получим значения 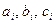, а, следовательно, и уравнение параболы на участке [x_i-1, x_i+1]. Уравнения парабол на разных отрезках [x_i-1, x_i+1] разные. 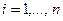. Квадратичная интерполяция является локальной интерполяцией.

Пример. Найти приближенное значение функции 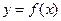при х = 0,32, если известна таблица ее значений, с помощью линейной и квадратичной интерполяции.

Решение.

1) С помощью линейной интерполяции.

х = 0,32 находится между узлами x_i-1 = 0,30 и x_i = 0,40. Найдем 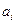и :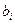

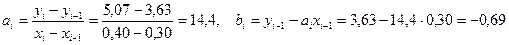, тогда уравнение прямой, соединяющей данные узлы, имеет вид .

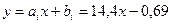Найдем значение функции в заданной точке: .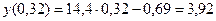

2) С помощью квадратичной интерполяции.

Ближайшими к х = 0,32 являются узлы x_i-1 = 0,15, x_i = 0,30, x_i+1 = 0,40. Составим систему для нахождения коэффициентов параболы, проходящей через данные узлы:

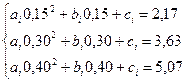
Решив систему, получим, что 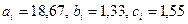. Подставим числа в уравнение параболы :

.

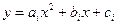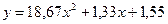Найдем значение функции в заданной точке: .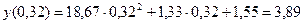

Многочлен Лагранжа/ Примером глобальной интерполяции являетсяпостроение интерполяционного многочлена, единого для всего отрезка[x₀, x_n], график которого проходит через все заданные в таблице точки. Это многочлен Лагранжа. Его уравнение имеет вид:

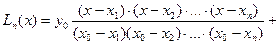
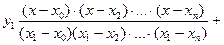
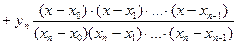- интерполяционный многочлен Лагранжа.

Оценка погрешности замены функции многочленом Лагранжа:

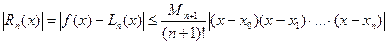, где .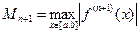

Решение предыдущего примера с помощью многочлена Лагранжа.

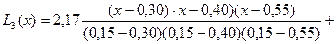
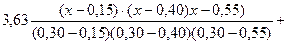
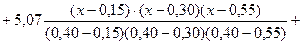
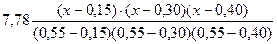= раскроем скобки и получим многочлен 3-ей степени.

Найдем значение функции в точке х = 0,32:

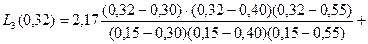
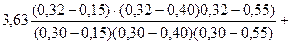
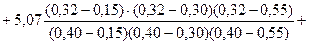
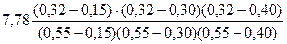= 3, 89.