п.3. Метод Рунге – Кутта
Метод Рунге – Кутта является одним из наиболее употребительных методов высокой точности. Метод Эйлера можно рассматривать как простейший вариант метода Рунге – Кутта.
Рассмотрим задачу Коши для дифференциального уравнения 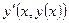 с начальным условием
с начальным условием 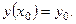 Как и в методе Эйлера, выберем шаг
Как и в методе Эйлера, выберем шаг 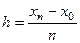 и построим сетку с системой узлов
и построим сетку с системой узлов 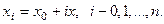 Обозначим через
Обозначим через 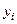 приближенное значение искомого решения в точке
приближенное значение искомого решения в точке 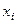 .
.
Приведем алгоритм метода Рунге-Кутта четвертого порядка точности:
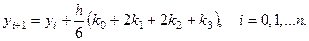
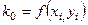 ,
, 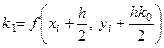 ,
,
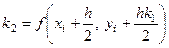 ,
, 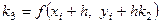 .
.
Оценка погрешности. Оценка погрешности метода Рунге – Кутта затруднительна. Грубую оценку погрешности дает правило Рунге. Так как метод Рунге – Кутта имеет четвертый порядок точности, т. е. p = 4, то оценка погрешности примет вид 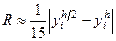 .
.
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши методом Рунге – Кутта четвертого порядка точности с заданной точностью 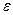 . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение
. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение 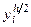 , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие 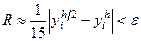 .
.
Приближенными решениями будут значения 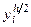 , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример.
Решить задачу Коши 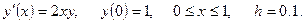
Решение.
Найдем 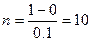 , тогда с учетом (6.20) расчетные формулы примут вид:
, тогда с учетом (6.20) расчетные формулы примут вид:
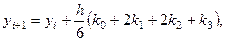
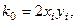
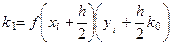 ,
,
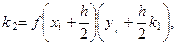
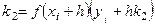 , i = 0, 1, …,10.
, i = 0, 1, …,10.
Задача имеет точное решение: 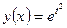 , поэтому погрешность вычисляется как абсолютная величина разности между точным и приближенным значениями
, поэтому погрешность вычисляется как абсолютная величина разности между точным и приближенным значениями 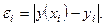
Найденные по формулам приближенные значения решения и их погрешности представлены в таблице
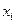
| 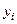
| 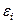
| 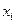
| 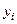
| 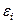
|
| 0.1 | 1.01005 | 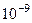
| 0.6 | 1.43333 | 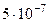
|
| 0.2 | 1.04081 | 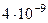
| 0.7 | 1.63232 | 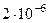
|
| 0.3 | 1.09417 | 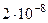
| 0.8 | 1.89648 | 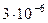
|
| 0.4 | 1.17351 | 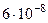
| 0.9 | 2.24790 | 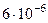
|
| 0.5 | 1.28403 | 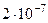
| 1.0 | 2.71827 | 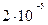
|
Дата добавления: 2016-06-15; просмотров: 2855;











