Понятие аппроксимации функции. Интерполяция
П.1 Основные понятия
Определение. Аппроксимировать функцию y = f(x) означает приближенно заменить ее некоторой другой функцией y = φ(x) так, чтобы отклонение φ(x) от f(x) в заданной области было наименьшим. Функция φ(x) называется аппроксимирующей функцией.
Для чего аппроксимировать функции?
Известны 4 способа задания функции: аналитический, графический, словесный и табличный. Табулируют те функции, вычисление которых, не смотря на их простоту, довольно громоздко (таблицы квадратов, логарифмов…). Также на практике часто встречаются случаи, когда функция y = f(x) задается не аналитически, а графически или таблично:
| x | x0 | x1 | x2 | ... | xn |
| y | y0 | y1 | y2 | ... | yn |
Так обычно получают функцию, описывающую исследуемый процесс, в результате эксперимента. Данные этого эксперимента заносятся или в таблицу, или на график, который иногда образуется и автоматически, в самопишущих приборах.
Характеристики таблиц: 1) название функций, значения которых они выражают; 2) объем таблицы (количество значений аргумента от начального значения до конечного), хi –называются узлами таблицы, a = x0 < x1 <…< xn = b – сетка таблицы; 3) шаг h, где h = хi - хi-1; 4) количество знаков табулируемой функции (вносят только верные знаки, абсолютная погрешность всех х одинакова); 5) конечная разность первого порядка уi - уi-1; 6) количество входов (равнозначно числу аргументов функции, то есть y = f(x) – таблица с одним входом).
Преимущества табличного способа: для каждого значения независимой переменной х, помещенной в таблицу, можно сразу же, безо всяких измерений и вычислений, найти соответствующее значение функции.
Недостаток табличного способа: не известен вид связи между х и у, то есть нельзя задать всю функцию сплошь, всегда найдутся такие значения независимой переменной, которых нет в таблице. Получить эти значения можно лишь путем очень сложных расчетов или проведения дорогостоящих экспериментов.
Задача, возникающая перед исследователем, состоит в отыскании соответствующего аналитического выражения для функции, используя информацию об уже известных ее значениях, и, как следствие, приближенного вычисления искомого параметра у при любом значении параметра х. Иначе: ставится задача получить по значениям функции, заданной в виде таблицы, аналитическое выражение функции. Этой цели и служит задача о приближении или аппроксимации функций. Конечно, в итоге получается не искомая функция f(x), а некоторая похожая на нее – j(x), то есть приближенная.
В процессе численной реализации этого подхода необходимо рассмотреть 4 основных вопроса: 1) вопрос об имеющейся информации относительно функции y = f(x), 2) вопрос о классе аппроксимирующих функций, то есть о том, какими функциями φ(x) будет аппроксимирована функция f(x), 3) вопрос о близости аппроксимируемой и аппроксимирующей функций, то есть о выборе критерия согласия, которому должна удовлетворять функция φ(x), 4) вопрос о погрешности, то есть об определении разности между точным и приближенным значениями.
В численном анализе широкое применение имеют 3 группы аппроксимирующих функций. Первая – класс всех многочленов степени не выше n. Вторую группу образуют тригонометрические функции 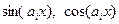 , порождающие ряды Фурье и интегралы Фурье. Третья группа состоит из экспоненциальных функций
, порождающие ряды Фурье и интегралы Фурье. Третья группа состоит из экспоненциальных функций 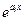 , определяющих явления типа распада и накопления.
, определяющих явления типа распада и накопления.
На практике самым распространенным и весьма важным случаем является аппроксимация многочленами 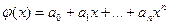 . При этом коэффициенты аi будут подбираться так, чтобы достичь наименьшего отклонения многочлена от заданной функции.
. При этом коэффициенты аi будут подбираться так, чтобы достичь наименьшего отклонения многочлена от заданной функции.
Одним из самых распространенных критериев согласия (или мерой отклонения) является критерий Чебышева: 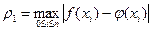 - максимальное отклонение функций в узлах хi.
- максимальное отклонение функций в узлах хi.
Если приближение строится на заданном множестве точек {хi}, то аппроксимация называется точечной. Если приближение строится на непрерывном множестве точек, например, на отрезке 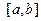 , то аппроксимация называется непрерывной или интегральной.
, то аппроксимация называется непрерывной или интегральной.
Выбор узловых точек, класса аппроксимирующих функций и критерия согласия должны быть подчинены одному вопросу – о требуемой точности. При построении приближения ставится жесткое условие: во всех точках отрезка 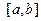 отклонение многочлена φ(x) от функции f(x) было по абсолютной величине меньше заданной величины
отклонение многочлена φ(x) от функции f(x) было по абсолютной величине меньше заданной величины 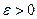 :
: 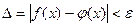 или
или 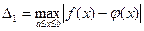 .
.
Дата добавления: 2016-06-15; просмотров: 4284;











