Дайте понятие интерполяции данных. Раскройте смысл следующих терминов: «сплайн-интерполяция», «билинейная интерполяция» и «двумерная интерполяция».
Под интерполяциейданных обычно понимают вычисление значений функции в промежутках между узловыми точками. Основная задача интерполяции-оценить значения представляемой данными зависимости в промежутках между ее узловыми точками.
Виды интерполяции:
-линейная
-билинейная
-сплайн-интерполяция
-одномерная интерполяция
-двумерная интерполяция
При линейной интерполяции зависимости y(x) узловые точки просто соединяются друг с другом отрезками прямых. При этом считается, что искомые промежуточные точки расположены на этих отрезках.
При сплайн-интерполяцииречь идет о применении функции, которая вместе с несколькими производными непрерывна на всей области определения, и на каждом отрезке этой области определения является некоторым алгебраическим многочленом. Для осуществления сплайн-интерполяции используется функция spline, которая имеет вид:
yi=spline(x,y,xi)
x-координаты по оси абцисс исходного, неинтерполированного сигнала
y- соответствующие х значения функции.
Функция spline интерполирует значения функции y в точках xi внутри области определения функции, используя кубические сплайны.
Под билинейной интерполяцией понимают расширение линейной интерполяции для функций двух переменных. Сначала проводят линейную интерполяцию в одном направлении, например, вдоль оси X, а затем –в направлении Y. Формулы билинейной интерполяции позволяют найти дополнительные координаты точек в произвольном прямоугольнике по координатам четырех его вершин, а затем интерполируют эту функцию на всю остальную фигуру. В MATLAB для этой цели служит функция shading interp, которая в программе должна быть записана после команды для визуализации объемной фигуры. Функция shading interp устанавливает раскраску каждой ячейки или грани цветами, которые определяются билинейной интерполяцией цветов в узлах сетки.
Для двумерной интерполяции поверхностей также может быть использована функция interp2. Эта функция интерполирует данные , определяющие некоторую поверхность на двумерной сетке {x,y}; При этом выходной массив zi может быть определен на более мелкой сетке {xi,yi}.
Функция interp2 записывается следующим образом:
zi=interp2(x,y,xi,yi,’method’)
Параметр ’method’ определяет вид интерполяции поверхности. При задании этого параметра в виде ‘nearest’ осуществляется ступенчатая интерполяция, или, как ее по другому называют, интерполяция методом ближайшего соседа. При такой интерполяции в качестве промежуточного значения выбирается ближайшее известное значение функции. Выбор ‘bilinear’ приводит к билинейной интерполяции, а‘bicubic’ – к сплайновой интерполяции поверхности.
7. Фракталы. Примеры фрактальных объектов. Фрактальность сигналов. Фрактальная размерность. Топологическая размерность. Самоподобие и самоаффинность.
Фракталами называются геометрические объекты:линии,поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Слово фрактал произошло от латинского слова fractus и переводится как дробный, ломанный. Самоподобие как основная характеристика фрактала означает,что он болееили менее единообразно устроен в широком диапазоне масштабов. При увеличении маленькие фрагменты фрактала получаются очень похожими на большие. В идеальном случае такое самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно растяжений, т.е. ему присуща дилатационная симметрия. Она предполагает неизменность основных геометрических особенностей фрактала при изменении масштаба.
Рассмотрим фрактальный объект, занимающий некую ограниченную область в Евклидовом пространстве. Пусть на каком-то этапе его построения он представляет собой множество из N точек, как-то распределенных в этой области. Разобьем всю область на кубические ячейки со стороной и объемом d. При уменьшении количество ячеек N(), покрывающих область, будет меняться по степенному закону
| N | , | (3.1) | ||
| D |
D называется хаусдорфовой или фрактальной размерностью.Логарифмируясоотношение (1) и устремляя к нулю, можно записать
| D lim | log N | . | (3.2) | |
| 0 | log |
Логарифм можно взять по любому положительному основанию, отличному от единицы, например, по основанию 10 или по основанию e2, 7183. (3.2)
и служит математическим выражением фрактальной размерности D. В соответствии с ним величина D является локальной характеристикой данного объекта. Фрактальная размерность является дробной величиной.
Одномерные фрактальные объекты имеют свойство самоподобия или масштабной инвариантности:части объекта подобны целому.Если число
определяющих переменных больше единицы и коэффициенты подобия по этим переменным различные, то такие фрактальные объекты называются самоаффинными. Самоаффинными фракталами могут быть также кривые формы сигналов от сложных генераторов, пространственного и временного энергетического спектров полупроводниковых тонких пленок и т.д.
8. Мультифракталы. Примеры мультифрактальных объектов. Мультифрактальная размерность. Самоподобие и самоаффинность фрактальных объектов.
Мультифракталы –наиболее сложных объектов нелинейной физики.
В природе распределение в пространстве параметров меры – аддитивной величины (длина, площадь, объем, масса, заряд, энергия и т.д.) – является сильно флуктуирующим, перемежаемым. Общие закономерности таких
явлений установлены теорией мультифракталов. Общепринятого определения мультифракталов нет. Приведем ряд утверждений, которые могут служить логическими компонентами строгого, обобщающего определения мультифракталов.
Перемежаемое распределение меры на геометрическом носителе связаны с мультифрактальными мерами.
Мультифрактальный объект характеризуется набором фрактальных размерностей.
Структурно - иерархически взаимосвязанные фрактальные объекты образуют мультифрактал.
Мультифрактальная размерность,или,обобщенная размерностьопределяется формулой Реньи
| D | lim | ln Nq, | (3.3) | |||
| q | q 10ln | |||||
| где – характерный размер ячейки множества, | N q,–минимальное |
число ячеек , содержащих меру и необходимых для покрытия исходного подмножества, q- порядок мультифрактального момента, принимающий
значения q Одна из интерпретаций физического смысла параметра q заключается в его эквивалентности обратной температуре(как
положительной, так и отрицательной).
В случайных фракталах самоафинность заключается в сохранении нормальности случайного распределения на разных масштабах, с различными дисперсиями.
Согласно идееПуанкаре «пространству» (или множеству) следует приписывать размерность n , если две его точки могут быть отделены удалением подмножества точек размерности n–1 (Рис.2.). Далее для обозначения размерности пространства (или множества) X будем использовать принятое обозначение Dim{X}=n.
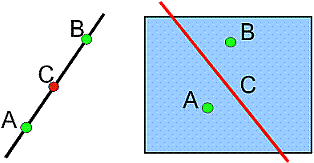 Рис.2.
Рис.2.
Отделение точек множеством меньшей размерности.
Исходя из этой идеи, определим индуктивную размерность следующим образом:
1. Dim{∅}= -1, ∅—пустоемножество.
2. Размерностьпространства X естьнаименьшеецелоечисло n, такое, чтокаждаяточкапространстваобладаетокрестностями, границыкоторыхимеютразмерность меньшую n.
Найдем согласно определению размерность точки. Ясно, что для отделения точки не требуется ничего. Следовательно, для ее отделения достаточно пустого множества {∅}. Тогдаразмерностьточкинаединицубольшеразмерностипустогомножества Dim{point}=1+ Dim{∅}=1 - 1=0. Такимобразом, размерностьточкиравна 0. Аналогичноможноустановитьтеперьразмерностьотрезкаиболеесложныхмножеств. Очевидно, чтоопределеннаятакимобразомразмерностьможетприниматьтолькоцелыезначения. Приразвитии теории размерности был обнаружен и другой путь ее определения. Для простоты изложим эту идею в двумерном случае. Рассмотрим двумерную область и разделим ее на маленькие ячейки, которые содержат свою границу (Рис. 3).
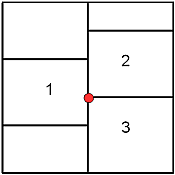 Рис.3.
Рис.3.
Покрытие квадрата ячейками.
Отмечена точка, принадлежащая сразу трем ячейкам. Меняя разбиение на ячейки нельзя добиться исчезновения таких точек, принадлежащих не менее чем трем ячейкам.
Легко заметить, что каковым бы ни было такое разбиение и форма ячеек, всегда найдутся точки, принадлежащие одновременно 3-м ячейкам. Это наблюдение привело к теореме Лебега-Брауэра: если n-мерная фигура разбита на достаточно малые ячейки, то непременно существуют точки этой фигуры, принадлежащие по меньшей мере n+1 ячейкам. Таким образом, приходим к определению размерности, которая сохраняется при непрерывных взаимооднозначных отображениях и является топологическим инвариантом. Это означает, что никакие множества не могут быть топологически эквивалентными, обладая разной размерностью. По этой причине определенную выше размерность также будем называть топологической размерностью пространства X . Теперь мы знаем, что топологическую размерность пространства можно определить двумя путям, отделяя две точки или покрывая его достаточно малыми ячейками. И здесь необходимо подчеркнуть два важных момента:
1. Топологическая размерность всегда целое число.
2. Для пустого множества её значение равно –1.
Динамические системы. Приведите примеры динамических систем. Динамический хаос. Математическая модель динамической системы. Отображение Пуанкаре. Логистическое отображение. Бифуркационные диаграммы. Показатели Ляпунова
Динамическая система – любой объект или процесс, для которого однозначно определено понятие состояния как совокупности некоторых величин в данный момент времени и задан закон, который описывает изменение (эволюцию) начального состояния системы с течением времени. Этот закон позволяет по начальному состоянию прогнозировать будущее состояние динамической системы, его называют законом эволюции.
Математическая модель динамической системы считается заданной, если введены параметры (координаты) системы, однозначно определяющие ее состояние, и указан закон эволюции.
• Закон эволюции динамической системы во времени записывается системой обыкновенных дифференциальных уравнений
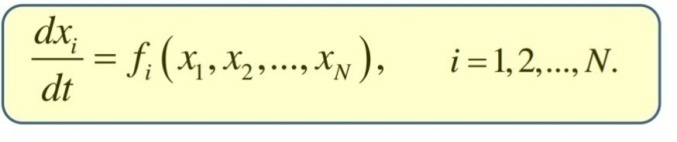
При математическом исследовании динамических систем отображением называют временную выборку данных
{х(t1), х(t2),…, х(tn), …,х(tN)}, для которой вводят обозначение хn ≡ х(tn). В простом детерминированном отображении:
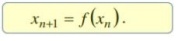
Это так называемое разностное уравнение.
Понятие отображения обобщается и на большее число переменных.
Предположим, например, что мы анализируем движение частицы, отображенное на фазовой плоскости [х(t), x (t)]. Если движение хаотично, то траектория стремится заполнить некоторую область фазового пространства.
Если хn х(tn) и у n x (tn), то эта последовательность точек
фазового пространства представляет собой двумерное отображение
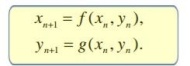
Если моменты выборки tn подчиняются определенному правилу, это отображение называется отображением Пуанкаре.
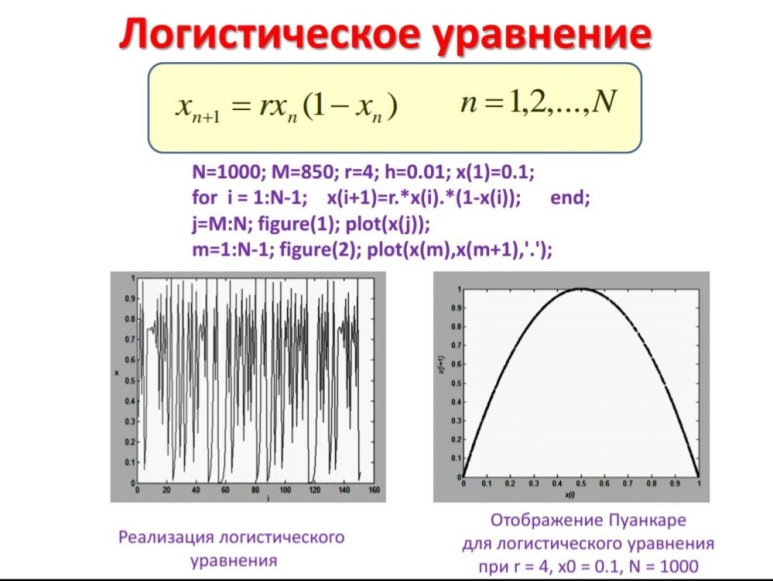
Путь к хаосу через удвоение периода. Когда наблюдается явление удвоения периода, в начальном состоянии система совершает основное периодическое движение. Затем, по мере изменения какого-либо параметра эксперимента r происходит бифуркация или изменение движения на периодическое с периодом, в два раза превышающим период исходных колебаний. С дальнейшим изменением r система подвержена последовательным бифуркациям, при каждой из которых период удваивается. Критические значения r, при которых происходят последовательные удвоения периода, подчиняются при п → ∞ следующему соотношению:

Это число называется числом Фейгенбаума
Процесс удвоения периода имеет точку сгущения вблизи некоторого критического значения параметра, после которого движение становится хаотическим.
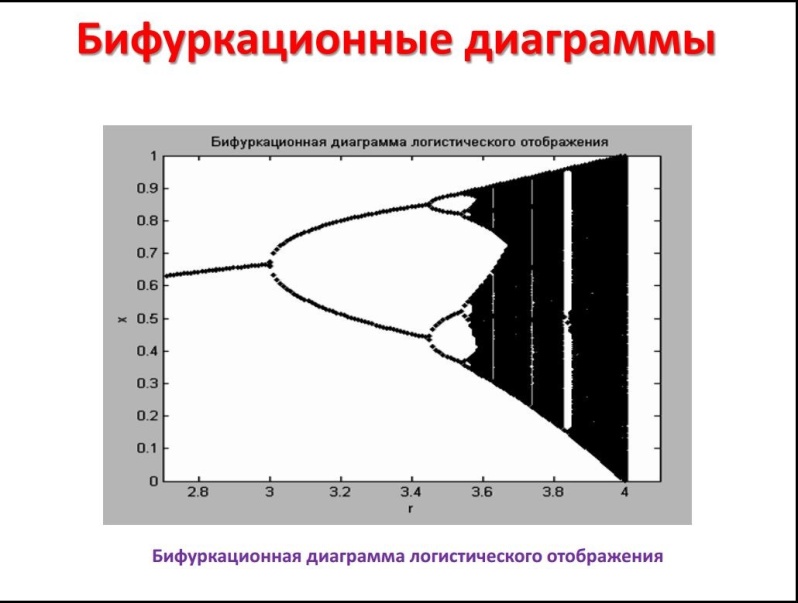
Хаос в детерминированных системах подразумевает чувствительную зависимость от начальных условий. Это означает, что две траектории, близкие друг к другу в фазовом пространстве в некоторый начальный момент времени, экспоненциально расходятся за малое в среднем время. Если d0 — мера начального расстояния между двумя исходными точками, то, спустя малое время t, расстояние между траекториями, выходящими из этих точек, становится равным
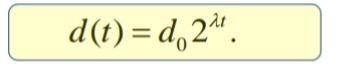
Если система описывается разностными уравнениями или отображением, то 0
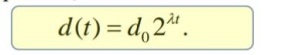
Величины и называются показателями Ляпунова.
Показатели Ляпунова
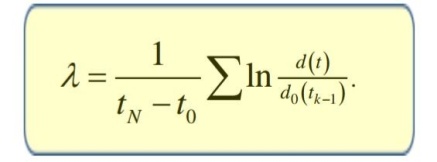
Критерий хаоса в терминах показателя Ляпунова принимает следующий вид: > 0 — хаотическое движение, 0 — регулярное движение.

Динамические системы. Раскройте смысл следующих терминов: «закон эволюции», «математическая модель динамической системы», «фазовая точка», «фазовая траектория». Опишите различия между следующими терминами: «линейная система» и «нелинейная система»; «консервативная система» и «неконсервативная система».
Динамическая система – любой объект или процесс, для которого однозначно определено понятие состояния как совокупности некоторых величин в данный момент времени и задан закон, который описывает изменение (эволюцию) начального состояния системы с течением времени. Этот закон позволяет по начальному состоянию прогнозировать будущее состояние динамической системы, его называют законом эволюции.
Математическая модель динамической системы считается заданной, если введены параметры (координаты) системы, однозначно определяющие ее состояние, и указан закон эволюции.
• Закон эволюции динамической системы во времени записывается системой обыкновенных дифференциальных уравнений
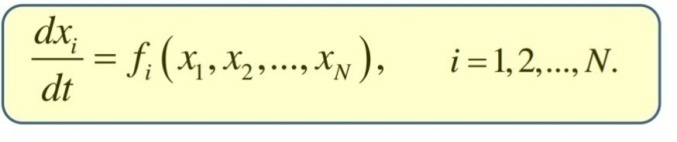
Под фазовым пространством понимают пространство, на котором представлено множество всех состояний системы так, что каждому возможному состоянию системы соответствует точка фазового пространства. В качестве координат для представления фазового пространства обычно используются обычные пространственные координаты (или обобщенные координаты, т.е. независимые между собой параметры любой размерности, число которых равно числу степеней свободы механической системы и которые однозначно определяют положение системы) и соответствующие значения импульсов. • Существование устойчивых траекторий в фазовом пространстве свидетельствует о наличии динамического хаоса в описываемой системе. Наличие в фазовом портрете замкнутых траекторий свидетельствует о периодическом характере колебаний, уходящие же в бесконечность фазовые траектории указывают на наличие в системе стохастичности.
Лине́йная систе́ма — любая система, для которой отклик системы на сумму воздействий равен сумме откликов на каждое воздействие. В математической модели линейной системы это означает, что оператор преобразования "вход-выход" линеен. Иногда линейное свойство системы называют принципом суперпозиции.
Нелинейная система — динамическая система, в которой протекают процессы, описываемые нелинейными дифференциальными уравнениями.
Консервативная система (от лат. conservo — сохраняю) — физическая система, работа неконсервативных сил которой равна нулю и для которой имеет место закон сохранения механической энергии, то есть сумма кинетической энергии и потенциальной энергии системы постоянна.
Дата добавления: 2017-06-13; просмотров: 2637;











