Кусочно-линейная интерполяция

При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости.

Для этого используется функция linterp (VX, VY, x). Для заданных векторов VX и VY узловых точек и заданного аргумента x функция linterp (VX, VY, x) возвращает значение функции при ее линейной аппроксимации. Графически это означает просто соединение узловых точек отрезками прямых. При экстраполяции используются отрезки прямых, проведенных через две крайние точки.

Пример

Пусть экспериментально получена амплитудная характеристика усилителя (таблица 6.1)

Таблица 6.1

В программной среде «MathCAD» исходная функция (U_ВЫХ=F(U_ВХ)) записывается в виде матрицы [2x8]:

Далее производится сортировка значений функции по возрастанию значений аргумента, если в таблице такая сортировка не произведена. Для этого обращаемся к встроенным функциям f(x), (например, на стандартной линейке).

Записываем:

V:=

Открываем окно f(x) и выбираем в разделе категория функций – «сортировка», а в разделе имя функции – «сортировка по аргументу» (csort (v, o)).

После щелчка на кнопке «ок» получим запись:

,

далее вставляем имя матрицы:

V:= csort (V,0)

Далее присваиваем значениям аргумента значения из первого столбца:

,

а значениям функции значения второго столбца:

Теперь можно провести кусочно-линейную интерполяцию.

Записываем:

W(x):=

Открываем окно встроенных функций. В разделе «категория функций» указываем название «интерполяция», а в разделе «имя функции» – «линейная» («linterp»). После щелчка по клавише «ок» появляется запись:

Вводим в скобки последовательно X,Y,x:

W(x):= linterp(X,Y,x)

Далее по правилам построения графиков строим зависимость W(x) = f(x) (Рис. 6.38).

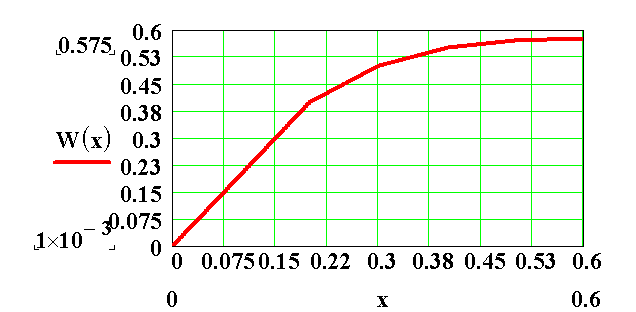
Рис.6.37 График зависимости W(x) = f(x)