Метод закраски Фонга (интерполяция нормалей). Преимущества и недостатки

В методе закраски, разработанном Фонгом, используется интерполяция вектора нормали N к поверхности вдоль видимого интервала на сканирующей строке внутри многоугольника, а не интерполяция интенсивности. Интерполяция выполняется между начальной и конечной нормалями, которые сами тоже являются результатами интерполяции вдоль ребер многоугольника между нормалями в вершинах. Нормали в вершинах в свою очередь вычисляются так же, как в методе закраски, построенном на основе интерполяции интенсивности. Как и выше, интерполяцию вдоль ребер можно выполнить поэтапно, вычисляя все три компоненты вектора нормали при переходе от каждой сканирующей строки к следующей. В каждом пикселе вдоль сканирующей строки новое значение интенсивности вычисляется с помощью любой модели закраски. Заметные улучшения по сравнению с интерполяцией интенсивности наблюдаются в случае использования модели зеркального отражения, так как при этом более точно воспроизводятся световые блики. Однако даже если зеркальное отражение не используется, интерполяция векторов нормали приводит к более качественным результатам, чем интерполяция интенсивности, поскольку аппроксимация нормали в этом случае осуществляется в каждой точке. В результате уменьшаются трудности, связанные с полосами Маха, однако значительно возрастают расходы. Общие черты и отличия методов Гуро и Фонга можно показать на примере цилиндрической поверхности, аппроксимированной многогранником (рис. 11). Пусть источник света находится позади нас. Проанализируем закрашивания боковых граней цилиндра.

Основные отличия можно заметить для закрашивания передней грани. Она перпендикулярна направлению лучей света. Поэтому нормали в вершинах этой грани располагаются симметрично — они образовывают попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обуславливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность одинакова (для линейной интерполяции). Это обуславливает единый цвет закрашивания. Все точки передней грани имеют одинаковый цвет, что, очевидно, неправильно.

Метод Фонга дает правильное закрашивание. Если интерполировать векторы нормалей передней грани, то по центру будут интерполированные нормали, параллельные лучам света (рис.12).

По методу Фонга центр передней грани будет светлее, чем края. Возможно, это не очень заметно на типографском отпечатке рисунка, однако это именно так. Чтобы закрасить куски бикубической поверхности, для каждого пиксела, исходя из уравнений поверхности, вычисляется нормаль к поверхности. Этот процесс тоже достаточно дорогой. Затем с помощью любой модели закраски определяется значение интенсивности. Однако прежде чем применить метод закраски к плоским или бикубическим поверхностям, необходимо иметь информацию о том, какие источники света (если они имеются) в действительности освещают точку. Поэтому мы должны рассматривать также и тени.

50. ТЕНИ

Алгоритмы затенения в случае точечных источников света идентичны алгоритмам удаления скрытых поверхностей! В алгоритме удаления скрытых поверхностей определяются поверхности, которые можно увидеть из точки зрения, а в алгоритме затенения выделяются поверхности, которые можно «увидеть» из источника света.

Поверхности, видимые как из точки зрения, так и из источника света, не лежат в тени. Те же поверхности, которые видимы из точки зрения, но невидимы из источника света, находятся в тени.Эти рассуждения можно легко распространить на случай нескольких источников света. Отметим, однако, что, используя такой простой подход, нельзя смоделировать тени от распределенных источников света. При наличии таких источников потребуется вычислять как тени, так и полутени. Поскольку алгоритмы затенения и удаления скрытых поверхностей одинаковы, представляется возможным обрабатывать описание объекта, используя лишь один из этих алгоритмов, последовательно применяя его к точке зрения и к каждому из точечных источников света. Совокупность полученных результатов позволяет определить, какие части объекта видимы наблюдателю и какие видны из одного или нескольких источников света. На основании этой информации осуществляется закраска сцены. Если правильно организовать вычислительный процесс, определение теней можно проводить лишь один раз для серии сцен, которые состоят из одних и тех же объектов, рассматриваемых с различных точек зрения. Источники света предполагаются неподвижными относительно объектов. Все это оказывается возможным потому, что тени не зависят от положения точки зрения.

В одном из способов построения тени к объекту добавляется второй, компланарныйему многоугольник, совпадающий с видимой (из источника света) частью много­угольника, принадлежащего объекту, если какой-либо из принадлежащих объекту многоугольников полностью или частично видим из источника света. Выделение второго многоугольника производится с помощью метода отсечения многоугольников.

Эти многоугольники детализации поверхности не принимаются во внимание при удалении скрытых поверхностей, однако используются при закраске. Если закрашивается часть многоугольника, которая видима из точки зрения и покрыта одним из таких много­угольников, следует учитывать как диффузное, так и зеркальное отражение, а также рассеянный свет. Та часть многоугольника, которая видима из точки зрения, но не покрыта многоугольником детализации поверхности, находится в тени и на ее закраску влияет только рассеянный свет. На рис. 11 показаны многоугольники детализации

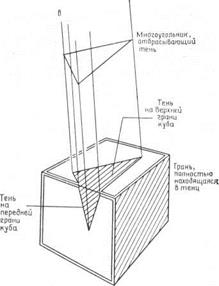(образовавшиеся на двух поверхностях куба) при частичном затенении треугольником.

Многоугольники детализации покрывают те части куба, которые видимы из источника света.

При другом способе построения теней,
называемом трассированием лучей,

рассматриваются поверхности, которые как пропускают, так и отражают свет. Этот метод описан ниже.