Геометрическая интерпретация(целочисленная решётка).
X
3 3
0 1 2 3 2 4 X1
Алгоритм решения базируется на отсечении дробных частей (причём не механически, а алгоритмически).
Наиболее эффективным алгоритмом решения целочисленных задач является алгоритм Гомори.
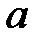
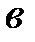 (а считается конгруэнтным
(а считается конгруэнтным 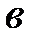 , если
, если 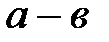 - целое число) .
- целое число) .
Алгоритм Гомори предусматривает 2 этапа:
Сначала используется обычный метод решения задач линейного программирования. При этом, если получается целочисленный ответ, то решение заканчивается, а если ответ не целочислен, то вводится дополнительное математическое ограничение, которое отсекает дробную часть искомой переменной.
Затем задача решается вновь с учётом нового ограничения обычными методами и т. д. На каждом последующем шаге решения, размер задачи и объём вычисления увеличивается (иногда до 100, иногда и до 1000 новых ограничений)и,  шагов решения. Не смотря на это, данный алгоритм самый эффективный.
шагов решения. Не смотря на это, данный алгоритм самый эффективный.
Пример: На предприятии необходимо установить новое оборудование. На его приобретение выделено 20 т. у. е. Имеющаяся S для установки – 38 м2. есть возможность приобрести оборудование 2-х видов – а и в. Стоимость а – 5000 у. е. , в – 2000 у. е. Sа – 8 м2, Sв – 4 м2. Производительность а – 7000 ед. за смену, в – 3000ед. за смену. !обеспечить max общую производительность.
х1 – количество ед – ц оборудования а.
х2 – количество ед – ц оборудования в.
Z = 7x1 + 3x2 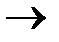 max
max
Ограничения:
1) 5х1 + 2х2 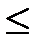 20 (у. е.)
20 (у. е.)
2) 8х1 + 4х2 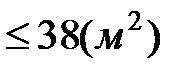
3) х1х2 – целые числа.
I.Решим задачу без учёта последнего ограничения симплекс – методом:
1) 5х1 + 2х2 + х3 = 20
2) 8х1 + 4х2 + х4 = 38
| Сj Ci | базис | Ро | х1 | х2 | х3 | х4 |
| х1 | -0,5 | |||||
| х2 | 7,5 | -2 | 1,25 | |||
| Zj - Cj | 0,25 |
Z = 7*1 + 3*7,5 = 29,5
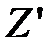 = 7*1 + 3*7 = 28
= 7*1 + 3*7 = 28
II.Для переменной, которая получилась не целочисленной, составим уравнение из последней симплекс – таблицы:
7,5 = 0х1 + 1х2 – 2х3 + 1,25х4 = 20
х2 = 7,5 + 2х3 – 1,25х4  0
0
-2 х3 + 1,25х4  7,5
7,5
т. к. х3 также должна быть целочисленной, то 2х3 можно опустить.
1,25х4 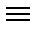 7,5
7,5
0,25х4 = 0,5; 1,5; 2,5…ограничения
Ограничения:
1) 5х1 + 2х2 + х3 = 20
2) 8х1 + 4х2 + х4 = 38
3) 0,5х4 – х5 = 0,5
х1 = 2
х2 = 5
х4 = 2
Z = 7*2 + 3*5 = 29
Если на втором шаге целочисленное решение не получилось, то надо было бы вводить следующее дополнительное целочисленное ограничение для нецелочисленной переменной.
Алгоритм решения: m=5; n=5; K1=4; K2=7; K3=2; K4=3; K5=10; Q1=600т.; Q2=2890т.; Q3=1100; Q4=2500; Q5 =300.
Задана Рij(верхний левый угол матрицы).
| j i | Qj Qi | |||||||||||
| Столбцы разности | ||||||||||||
| 3,5 к.р | 0,5кр | 380-220 | ||||||||||
| 3,35 к.р | 1,55кр | 2,1кр | ||||||||||
| 1кр | ||||||||||||
| 3кр-1560 | ||||||||||||
| 3,25кр | 6,75кр | |||||||||||
| …….. разности | ||||||||||||
1. Необходимо расписать целевую функцию и ограничения с заданными параметрами.
2. В каждой строке и столбце матрицы определяется разность между двумя лучшими показателями (между max производными) и заносим значения разности в строку, столбец разности.
3. После определения разностей, выбираем наибольшую величину разностей, при этом не имеет значения, где они находятся. Против выбранной разности ставим перегрузочные машины на тот причал, на котором достигается max производительность (в эту клетку ставится max количество кранов).
4. После постановки кранов на причал вычеркивается в таблицы. Строка, столбец с заполненным квадратом. Строка вычеркивается, если расставлены все краны соответственного типа. Столбец тогда, если выполнен заданный грузооборот на причале.
5. Далее снова определяется разность двух лучших показателей в оставшихся строках и столбцах матрицы.
Новые значение разностей размещаются в следующем столбце, строке разностей. Действие данного алгоритма повторяется до тех пор, пока не будет, выполнен грузооборот на всех причалах или не будет расставлены все краны по причалам.
Числовое решение в матрице.
В результате решения получилось, что весь грузооборот можно выполнить без использования 1 крана третьего типа. После получения решения необходимо рассчитать значения целевой функции и проверить ограничения.
1. 3,30*180=600 2. 3,5+0,5=4
23,5*380+3*520=2890 3,35+1,55+2,1=7
3,25*340=1100 1<2
1,55*260+6,75*310=2500 3=3
0,5*80+2,1*90+1*70=300 3,25+6,75=10
Метод аппроксимации часто применяется для составления исходного плана задачи в матрицах большого размера. Для получения строго оптимального плана расстановки необходимо  решение закончить точным методом линейного программирования. Сравнительный показатель трудоемкости данного
решение закончить точным методом линейного программирования. Сравнительный показатель трудоемкости данного  и
и  точного метода = 50.
точного метода = 50.
Приближенный метод решения задач линейного программирования. Метод индексов.
Наиболее часто использовалось при решении задач операции планирования, при этом достигается достаточно  к оптимальному решению. Возникновение таких методов вызвано тем, что частые измерения в оперативном плане сделали непрактичным использование трудоемких, точных методов.
к оптимальному решению. Возникновение таких методов вызвано тем, что частые измерения в оперативном плане сделали непрактичным использование трудоемких, точных методов.
Индексный метод является самым простым  методом линейного программирования, с его помощью задачи и решаются быстро, с min затратами труда и времени. Он основан на сопоставлении степени целесообразности использование технических средств на том или ином участке работы. Сопоставление производится с помощью индексов.
методом линейного программирования, с его помощью задачи и решаются быстро, с min затратами труда и времени. Он основан на сопоставлении степени целесообразности использование технических средств на том или ином участке работы. Сопоставление производится с помощью индексов.
Недостаток: при решении задачи сопоставляется показатели однотипных технических средств на различных участках работы. При этом сопоставление различных технических средств на каждом из участков работы не производится. Т.е. сопоставление показателей матрицы производится по строкам и не производится, по столбцам  индексный метод обеспечивает результаты решения менее точные, чем метод простой аппроксимации.
индексный метод обеспечивает результаты решения менее точные, чем метод простой аппроксимации.
Постановка задачи:
m – количество типов грузовых судов i=1,…, m
n – количество грузовых линий движения j=1,…,n
Фi – количество судов каждого типа
Qj – грузооборот на каждой линии (мил. т/км)
Pij – провозная способность судна i-го типа на j-той линии
(мил. т/км)
Цель: необходимо так расставить имеющийся флот по линиям, чтобы выполнить заданный грузооборот min количеством судов.
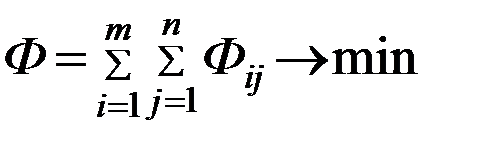
Ограничения:
1. 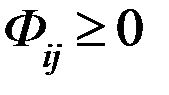
2. 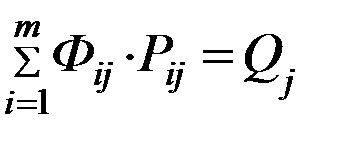
3. 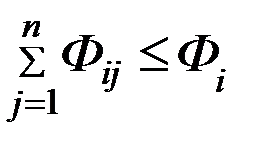
Алгоритм решения рассматриваем на примере:
m=3; n=5; Ф1=6; Ф2=8; Ф3=12 ……………………….
Задача Рij (в матрице)= 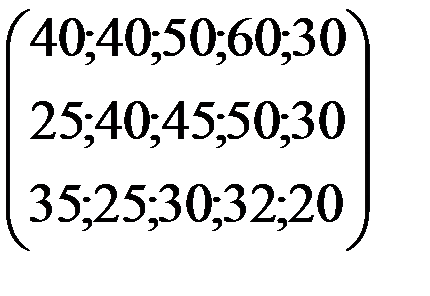
1). Исходные данные размещаем, в матрице при этом типы судов размещается, в порядке ухудшения показателей
| i | j | |||||
| Gj Фi | ||||||
| 0,33 | 0,33 | 0,17 | 1) 60 40 | 6) 36 20,4 | ||
| 0,5 | 4) 40 20,2 | 3) 45 60,1 | 0,4 | |||
| 2) 35 30 | 5) 25 60,29 | 0,14 | 0,09 | 0,43 |
2) Определяем значение индексов.

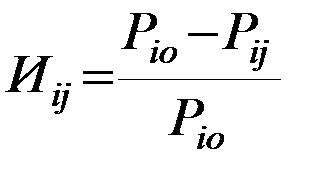
Где Pio- провозная способность судна i-го типа на базисной линии.
За базисную линию для судов каждого типа принимается та линия на которой достигаются лучшие показатели (max Pij) каждый тип судна может иметь свою базисную линию.
Если задача решается по показателю эксплуатационных расходов или себестоимости, то индексы определяются так:
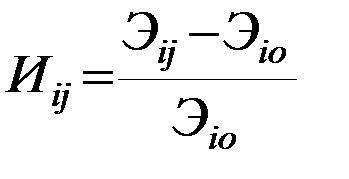
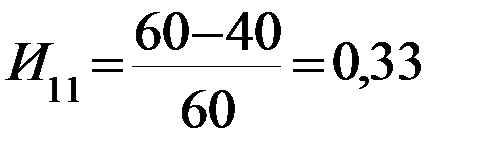
Индекс- это число, показывающее относительные потери провозной способности судов при использовании их на других линиях кроме базисной. Индекс может рассмотреть как штраф, накладываемый за использование судов на других линиях по сравнению с базисной. Чем ближе значение индекса к Ø, тем эффективнее использование судов на данной линии. По этому признаку и осуществляется распределение судов по линиям.
Распределение начинается с судов, имеющих лучшие показатели.
На базисной линии закрепилось max возможное количество судов. Если ….. грузооборот на данной линии, то вычеркивается столбец; если распределены все суда данного типа, то вычеркивается строка.
Далее суда ставятся на ту линию, где имеется min значение индекса из всех индексов матрицы, оставшихся после вычеркивания.
Шаги решения повторяются до тех пор, пока не будет вычислен грузооборот на всех линиях или будут расставлены все суда.
3) После расстановки судов по линиям определяем сколько потребовалось судов для выполнения заданного грузооборота, как в целом, так и по типам флота.
В примере объем перевозок на всех линиях выполнен при остатке 1,5 судов третьего типа в резерве.
Ф=8+6*10,5=24,5 Проверка ограничений: 3*35=105
4+2=6 2*40+6*25=230
2+6=8 6*45=270
3+6+1,5<12 4*60=240
2*36+1,45*20=100
Для получения оптимального решения необходимо полученное решение закономерность одним из точных методов.
Модифицированная распределительная задача.
Экономическая постановка и математическая модель. Условия оптимального плана.
Эту же задачу называют обобщенная транспортная задача.
На РТ обобщенная транспортная задача применяется для оптимального распределения транспортных и перегрузочных средств по участкам работы.
Обобщенной задачей называется потому, что при ее решении используются условия оптимальности в общем виде.
Алгоритм решения обобщенной транспортной задачи рассмотрим на примере распределения судов по линиям.
m- (типов судов) i=1, …,m
n – (линий движения) j=1, …, n
Фi - количество судов каждого типа
Пij – пассажирооборот на каждой линии за навигацию
(мил. пас/км)
Фij – количество судов i- го типа закрепленного за j- той линией
Zij – провозная способность судна i- го типа на j- той линии за навигацию (мил. пас/км)
Эij – эксплуатационные расходы по судну i- го типа на j- той линии за навигацию (тыс. руб.)
Необходимо составить такой план расстановки судов по линиям, при которой Эij 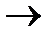 min.
min.
Целевая функция: 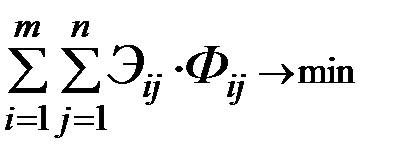
Ограничение: Фij 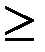 0
0
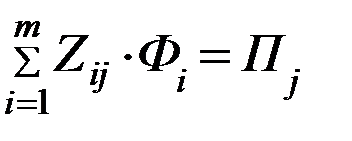
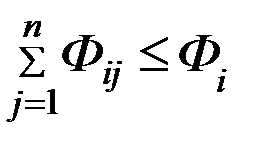
Условия оптимальности обобщенной транспортной задачи: план расстановки судов по линиям будет оптимальным, если следующие требования:
1) 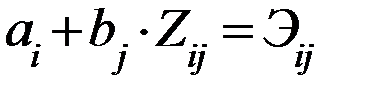 для Фij>0 (для заполненных клеток)
для Фij>0 (для заполненных клеток)
2) 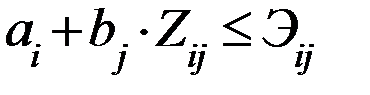 для Фij=0
для Фij=0
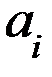
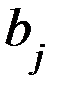 - потенциалы (оценочные числа)
- потенциалы (оценочные числа)
С помощью первого уровня определяются все значения 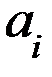 и
и 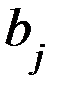 , а с помощью второго неравенства проверяется оптимальность плана.
, а с помощью второго неравенства проверяется оптимальность плана.
Пример: m=2, n=3, П1=9, П2=3, П3=6 (мил. пас/км)
Z12=Z22=1 (мил. пас/км) Э11=22, Э12=14, Э13=26
Z12=Z21=1,5 Э21=16, Э22=12, Э23=20
Z13=Z23=2 Ф1=5, Ф2=7
Составляем первоначальный план расстановки в соответствии с условиями допустимости, при этом количество заполненных клеток должно быть = m+n-1 (2+3-1)=4
| j | |||||
| i | nj | ||||
| Фi | bj a i | 14,5 | 18 14 | ||
| 1,5 5- | +3 14 ** | ||||
| -6 | 1,5 16 4 + | 12 - |
Проверка условия оптимальности: 0+18*1 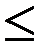 14 – не выполняется
14 – не выполняется
0+13*2=26 – выполняется
Проверка оптимальности второго типа: 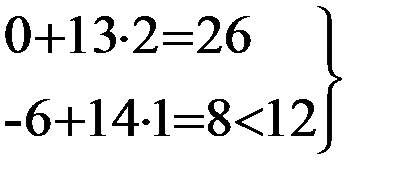
 план оптимальный
план оптимальный
Проверка ограничений и расчет условий функции:
Э=2*22+3*14+4*16+3*20=210 тыс.руб.
III часть. Системы массового обслуживания (СМО)
Потоки событий
Понятие потока событий. Простейший поток.
В процессе деятельности координаты элемента системы меняются. Под функцией будут понимать периодическую смену состояний элемента, а значит и координат этого элемента.
Под событием будут понимать  изменения состояния элемента системы, т.е.
изменения состояния элемента системы, т.е.  изменения координат . Т.е. функция – это процесс событий, т.е. последовательное нарастание событий.
изменения координат . Т.е. функция – это процесс событий, т.е. последовательное нарастание событий.
Под случайным событием будут понимать такое событие, координаты каждого нельзя точно предсказать.
Пусть X(t) мы точно предсказать не можем, тогда случайным событием называется множество значений величины 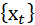 , зависящих от параметра t.
, зависящих от параметра t.
При изучении экономических систем в качестве параметра t обычно выступает время, а под X понимаются координаты состояния системы, т.е. экономические показатели.
Потоком событий называется упорядоченная последовательность случайных событий (события являются случайными, а их последовательность упорядоченной).
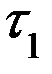
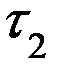
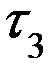
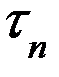
 (временная ось)
(временная ось)
через 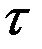 - моменты операции
- моменты операции
f.e. 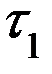 - момент прибытия судна
- момент прибытия судна
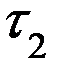 - начало обработки
- начало обработки
Их очередность строго упорядочена, а каждая 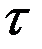 (ее величина) случайна.
(ее величина) случайна.
Потоки событий делятся на несколько классов.
1). если число событий, происходивших в фиксированный интервал времени Т зависит от величины этого интервала и не зависит от начала его отчета, то такой поток называется стационарным.
2). если поток событий, происходивших за интервал Т зависит от величины этого интервала, но не зависит от того, когда и каким образом система пришла в исходное состояние, то поток называется потоком безпоследействия.
3) Ординарным называется такой поток событий, в котором вероятность появления двух или более событий в течении элементарного отрезка времени (d T) пренебрежимо мала, по сравнению с вероятностью наступления одного события.
Стационарный ординарный поток событий безпоследействия называется простейшим потоком или потоком Пуассона.
Реальные процессы редко можно представить в виде пуассоновских, но для простейших потоков разработан хороший математический аппарат, который помогает решать многие экономические задачи, поэтому желательно приведение реальных потоков к простейшим.
Для этого используется два искусственных приема:
1). Метод агрегирования (т.е. состоит в укрупнении событий)
2). Метод дифференцирования (т.е. расчленение событий на несколько)
У простейшего потока математическое ожидание числа событий за какой-то интервал времени t распределено по закону Пуассона.
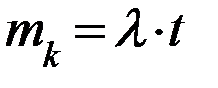
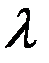 - это плотность потока, т.е. математическое ожидание появления числа событий в единицу времени.
- это плотность потока, т.е. математическое ожидание появления числа событий в единицу времени.
Практически 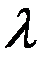 рассчитывается как среднее число событий в единицу времени.
рассчитывается как среднее число событий в единицу времени.
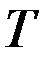 - интервал времени между двумя смежными событиями (случайная величина).
- интервал времени между двумя смежными событиями (случайная величина).
В простейшем потоке величина Т распределена по ……….. (показательному) закону.
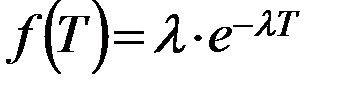
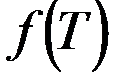 - плотность вероятности распределения
- плотность вероятности распределения
Математическое ожидание: 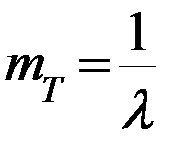
Дисперсия: 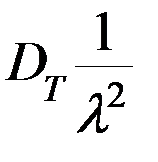
Среднеквадратическое отклонение: 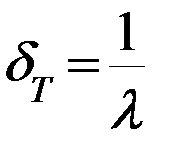 , т.е.
, т.е. 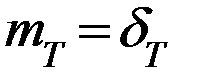
Равенство 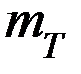 и
и 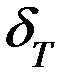 используется при рассмотрении реального потока в виде простейшего.
используется при рассмотрении реального потока в виде простейшего.
Понятие Марковских процессов. Их классификация.
Случайный процесс будет называется Марковским в том случае, если случайное событие, происходящее с системой, зависит от времени после начала отчета интервала и не зависит от того сколько и каких событий произошло до начала отсчета этого интервала, т.е. поток событий должен быть обязательно без последствий.
Если  -ет последовательность t1<t2<,….<tn отсчетов времени и при этом соблюдается следующие условия:
-ет последовательность t1<t2<,….<tn отсчетов времени и при этом соблюдается следующие условия:
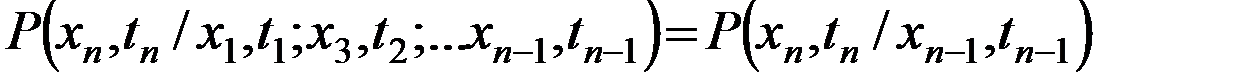
Т.е. условная вероятность того, что на n- ном шаге отчета времени будет зафиксированы координаты xn при условии, что на первом шаге будут зафиксированы координаты x1 на втором x2, на n-1м-x-1 и эта условная вероятность будет = условной вероятности того, что на n-ном шаге будут зафиксированы координаты xn, если на n-1-вом шаге зафиксированы координаты xn-1.
Различают два вида Марковских процессов:
1). Марковский процесс с дискретным временем.
с непрерывным временем
Моделирование Марковского процесса с дискретным временем.
Для данного вида Марковского процесса характерно, что изменение координат системы не происходить в какие-то фиксированные моменты времени.
Введем обjзначения:
S – состояние системы
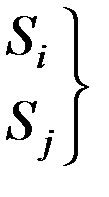 различные координаты системы (под i-м понимается начальное состояние системы, под j-м последующее)
различные координаты системы (под i-м понимается начальное состояние системы, под j-м последующее)
Для состояния Si  - ет набор координат (показателей)характерных положений в данный момент
- ет набор координат (показателей)характерных положений в данный момент
Pij – вероятность того, что система из i-го состояния перейдет в j-тое.
Марковский процесс можно задать двумя способами:
1). с помощью матрицы вероятностей перехода
2). с помощью размеченного графа состояний
Переход из 1 во 2 и т.д.
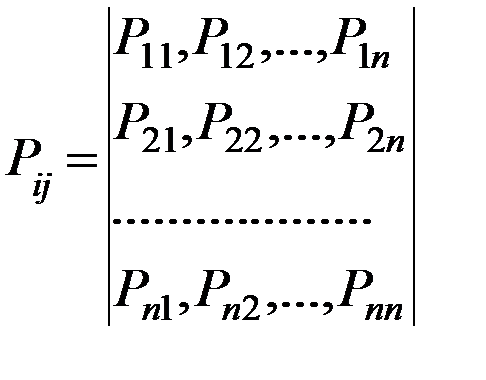 (полная группа событий)
(полная группа событий)
Каждый элемент данной матрицы отражает вероятность перехода из i-го состояния в j-тое.
Можно записать: 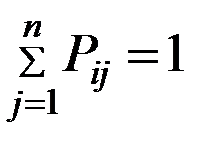
Когда система может находиться в наибольшем числе состояний, т.е. n …….. мало, то наиболее удобно описать Марковский процесс с помощью второго метода (размеченного графа состояний)
| S5 |
| S3 |
| S2 |
| S4 |
| S1 |
P13
P11 P14 P25 P52
P35
P53
P45
Задание Марковского процесса с помощью размеченного графа состояний удобно по двум причинам:
1) не надо отражать  - цие связи, т.е. когда Pij= Ø
- цие связи, т.е. когда Pij= Ø
2) нет необходимости указывать переход системы в это же состояние (из i-го в j-тое т.е. Pij)
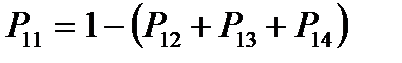
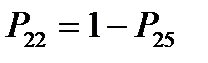 и т.д.
и т.д.
Это более экономичный способ
Введем еще обозначения:
Pi(K) – это вероятность того, что система на котором шаге будет находится в i-том состоянии
 в начальный момент времени система находится в первом состоянии.
в начальный момент времени система находится в первом состоянии.
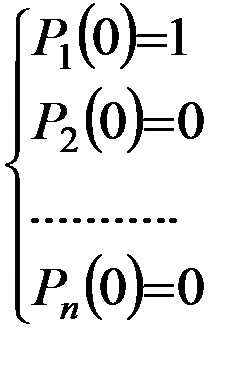
/>Вероятность того, что система на первом шаге и останется в первом состоянии Р1(1) = вероятности перехода из первого состояния в первое (Р11) Р1(1)=Р11.
Вероятность того, что система на первом шаге перейдет во второе Р2(1)=Р12, на первом шаге перейдет из первого в n-ное состояние =Р1n Р2(1)=Р12
Рn(1)=P1n
На втором шаге система перейдет в одно из возможных n-ных состояний, но все зависит от того, в каком состоянии система находится на предыдущем, т.е. на первом шаге.
Выдвинем следующие гипотезы:
- вероятность того, что на втором шаге система будут находиться в первом состоянии
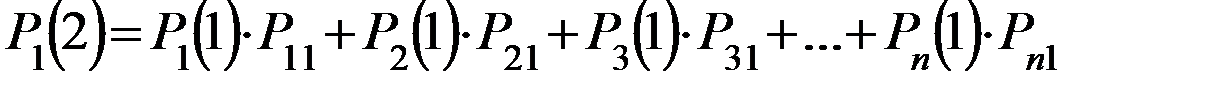
- вероятность того, что на втором шаге система будет находиться в первом состоянии
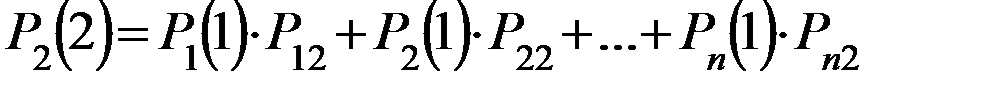
По аналогии 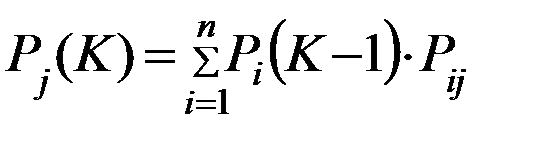
Моделирование Марковского процесса с непрерывным временем
Марковский процесс, в котором состояние системы может меняться в  случайный момент времени называется Марковским процессом с непрерывным временем.
случайный момент времени называется Марковским процессом с непрерывным временем.
Необходимо знать вероятности нахождения системы в i-том состоянии в  момент времени:
момент времени: 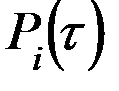
На практике с помощью статистических наблюдений мы можем только установить условные вероятности такого вида, которые обозначают, что система из состояния I перейдет в состояние j за время t.
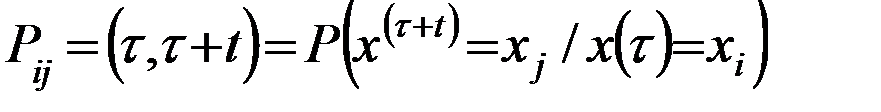
Рассмотрим поток случайных событий:
t
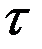
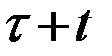

Для марковских процессов с непрерывным временем характеристикой процесса может быть только мгновенная характеристика – плотность вероятности перехода.
В Марковских процессах, как и в простейших, временные интервалы между соседними случайными событиями распределены по показательному закону:
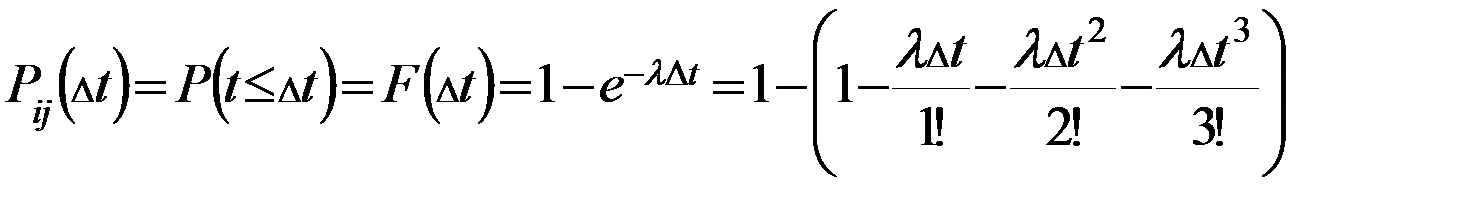
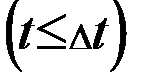 - вероятность того, что событие наступит за интервал
- вероятность того, что событие наступит за интервал 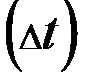 в момент
в момент  .
.
Все слагаемые в скобках, начиная с 3 представляют собой величины бесконечно малые относительно второго слагаемого в скобке ( 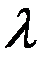 ), поэтому ими можно пренебречь и записать следующим образом:
), поэтому ими можно пренебречь и записать следующим образом:
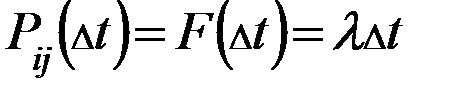 - вероятность того, что за промежуток
- вероятность того, что за промежуток 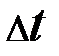 произойдет переход из i-го состояния в j-тое =
произойдет переход из i-го состояния в j-тое = 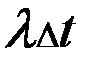
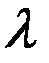 - параметр показательного значения, т.е. величина оборотная математическому ожиданию, (плотность потока).
- параметр показательного значения, т.е. величина оборотная математическому ожиданию, (плотность потока).
Вероятность того, что за промежуток 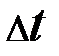 не произойдет никакого события, т.е. система, находившаяся в i-том состоянии, из него не выйдет:
не произойдет никакого события, т.е. система, находившаяся в i-том состоянии, из него не выйдет:
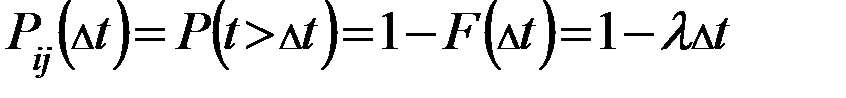
Марковские процессы будут однородными и неоднородными
Неоднородные процессы- это если плотности вероятности переходов зависят от времени.
Однородные- плотности вероятности переходов не зависит от времени.
Для неоднородных Марковских процессов математический аппарат до сих пор не разработан.
Уравнение Колмогорова-Чепмена
Однородный и непрерывный во времени Марковский процесс описывается системой дифференцирования уравнений Колмогорова – Чепмена.
Вывод этих уравнений построим применительно к системе, представленной на рис.
| S1 |
| S4 |
| S3 |
| S2 |
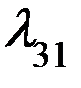
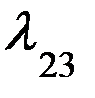
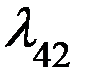
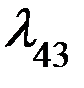
В начале отчета времени, равно t придадим ему малое приращение  и будем рассматривать вероятности того, что за этот промежуток
и будем рассматривать вероятности того, что за этот промежуток  система будет переходить в то или иное возможное состояние.
система будет переходить в то или иное возможное состояние.
Вероятность того, что система за время  перейдет в первое состояние.
перейдет в первое состояние.
Гипотезы:
1).В момент времени t находиться в первом состоянии
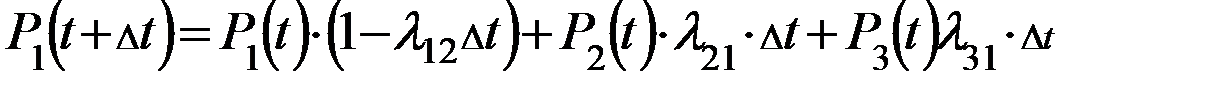
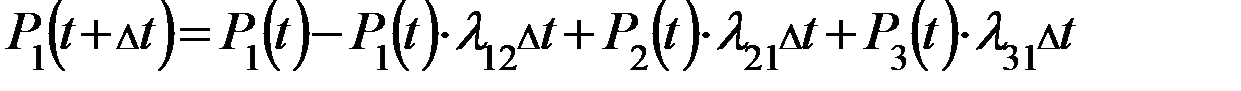
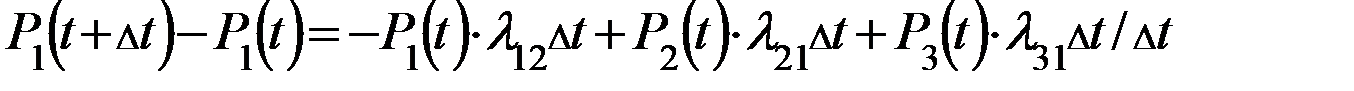
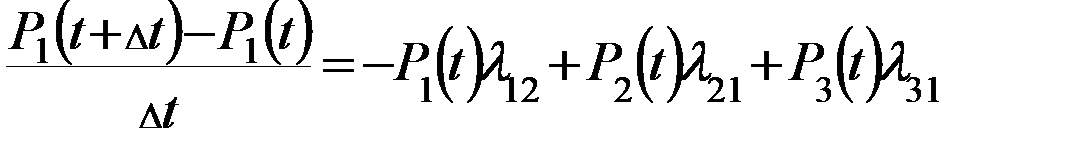
И за 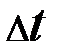 не пере….. никуда, т.е. ….. в S2
не пере….. никуда, т.е. ….. в S2 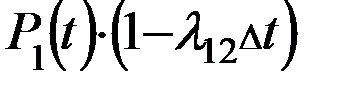
Левая часть уравнения – это приращение функции к приращению аргумента 
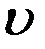 изменения по t
изменения по t  производная по t.
производная по t.
Выведенное последние дифференцированное уравнение характеризует вероятность нахождения системы в  момент времени в состоянии 1.
момент времени в состоянии 1.
(1) 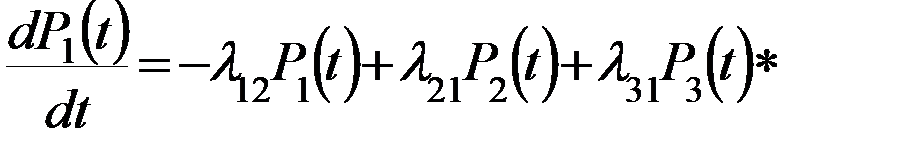
Дифференцированное уравнение (*) характеризует вероятность нахождения системы в  момент времени в состоянии 1. Аналогично для второго состояния.
момент времени в состоянии 1. Аналогично для второго состояния.
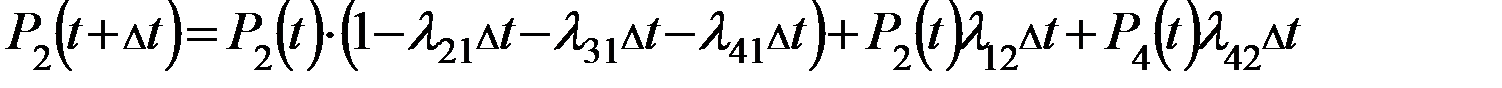
Произведем преобразование:
(2) 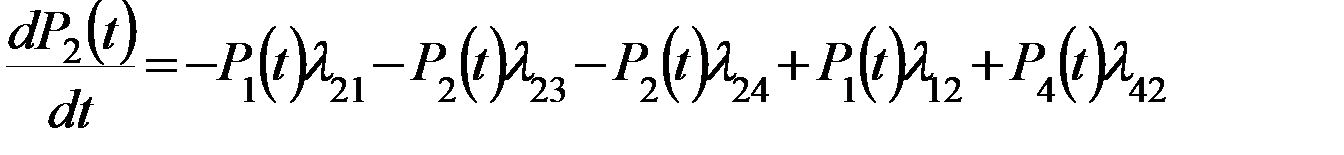
Мнемонические правила (по ассоциации) построения уравнений Колмогорова-Чепмена:
1. Каждое уравнение представляет собой дифференцированное уравнение, в левой части которого стоит производная по времени вероятности, нахождение системы в  из возможных соотношений.
из возможных соотношений.
2. Правая часть содержит столько членов, сколько ненулевых связей содержит матрица вероятностей переходов или размеченный граф состояний (для данного состояния).
3. Каждый член правой части уравнения представляет собой произведение плотности вероятности перехода из данного или в данное состояние ( 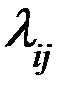 ) на вероятность нахождения системы в состоянии из которого связь исходит.
) на вероятность нахождения системы в состоянии из которого связь исходит.
4. Если связь исходит из данного состояния, то перед этим членом уравнения стоит знак «-», а если связь входит в данное состояние, то соответственно стоит знак «+».
(3) 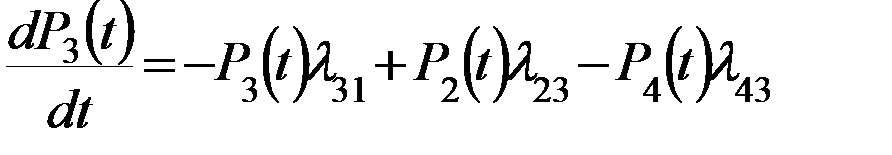
(4) 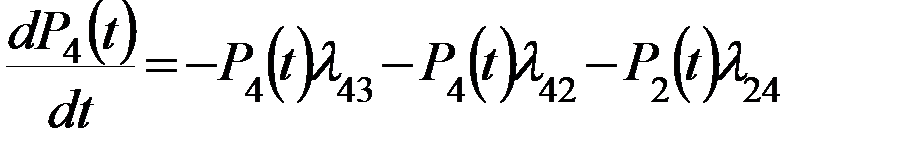
Эти 4 уравнения (1), (2), (3), (4) позволяющие определить вероятность нахождения системы в  из возможных состояний в
из возможных состояний в  момент времени называется системой Колмогорова-Чепмена (К-Ч)
момент времени называется системой Колмогорова-Чепмена (К-Ч)
Понятие установившегося режима работы.
Под установившимся режимом понимается такое функционирование системы, которое не зависит от времени, т.е. мы оперируем средними вероятностями. Эти средние вероятности называются предельными вероятностями.
Для того чтобы из системы уравнений К-Ч получить предельными вероятности, мы правая часть уравнений приравниваем к Ø и избавляемся от моментов времени (t).
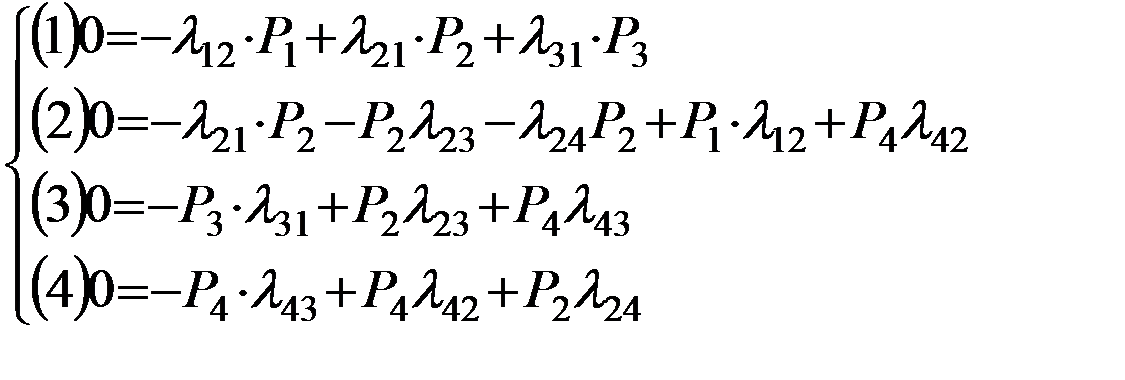
Тогда система дифференцированных уравнений преобразуется в систему линейных уравнений:
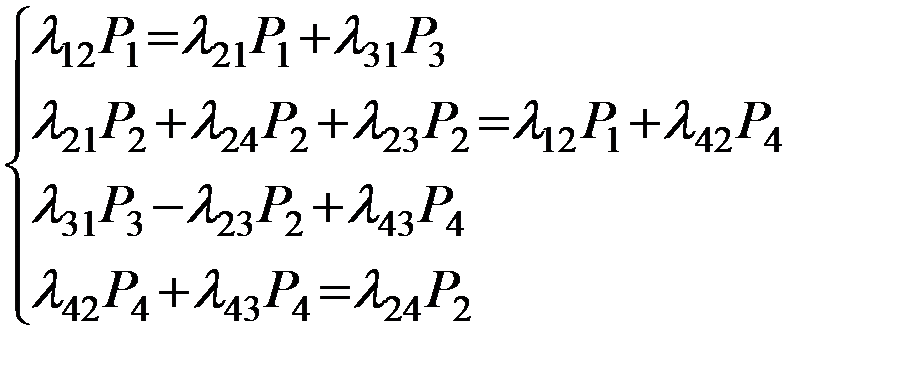
Не всякая реальная система имеет установившийся режим функционирования. Правила или признаки, при которых система имеет установившийся режим:
- число взаимосвязанных состояний системы должно быть конечным
- в каждое из возможных состояния система может перейти из  в другое взаимное состояние (может быть непосредственно, а может быть через другое состояние).
в другое взаимное состояние (может быть непосредственно, а может быть через другое состояние).
Рассмотрим пример: имеется причал, на котором осуществляется выгрузка угля из судов с помощью двух портовых кранов.
Система может находится в одном из следующих состояний:
S1 - оба крана в рабочем состоянии и осуществляют выгрузку
S2 - оба крана в рабочем состоянии, но выгрузку не осуществляют
S3 – 1 кран осуществляет выгрузку, 1 ремонтируется
S4 – оба крана ремонтируются
Графическое состояние данной системы
| S1 |
4 4
| S3 |
| S4 |
| S2 |
2 1
 на основе анализа фактических данных установлено, что поток груженных углем судов в порт равен
на основе анализа фактических данных установлено, что поток груженных углем судов в порт равен 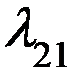 = 4 суд/сут.
= 4 суд/сут.
Средняя продолжительность выгрузки судна двумя кранами составляет 4 часа или1/6 суток, а одним краном 8 часов или 1/3 суток. Тогда интенсивность потоков событий, заключается в отходе порожних судов от причала составляет 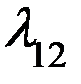 = 6 суд/сут. Если 1 кран сломался, то
= 6 суд/сут. Если 1 кран сломался, то 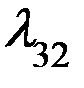 = 3 суд/сут.
= 3 суд/сут.
Необходимость профилактического осмотра механизмов кранов и различных непредвиденных его ремонтов возникает в среднем 4 раза в сутки 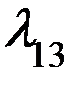 = 4 раза/сут.
= 4 раза/сут.
Интенсивность потока отказов одновременно два кранов составляет 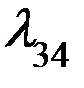 = 1 ремонт/сут.
= 1 ремонт/сут.
Средняя продолжительность ремонта или осмотра каждого крана  1 час или 1/24 суток
1 час или 1/24 суток 
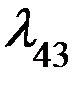 =24.
=24.
Поток восстановлений одновременно обоих ремонтных кранов 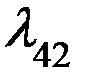 = 2 восстановления/суток.
= 2 восстановления/суток.
Необходимо определить относительную продолжительность нахождения причала в каждом из возможных состояний при установившемся режиме его работы.
Т.к. система имеет установившийся режим, то можно записать линейное уравнение предельных вероятностей состояний системы:
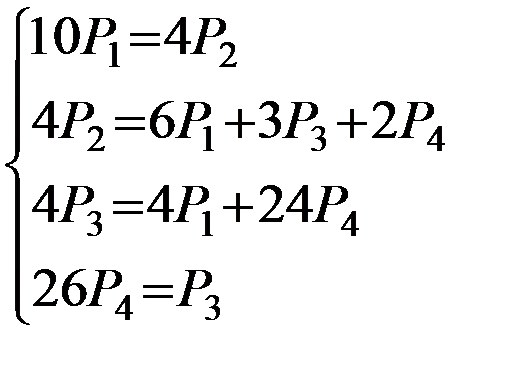
Выразим все переменные через одну Р3=26Р4
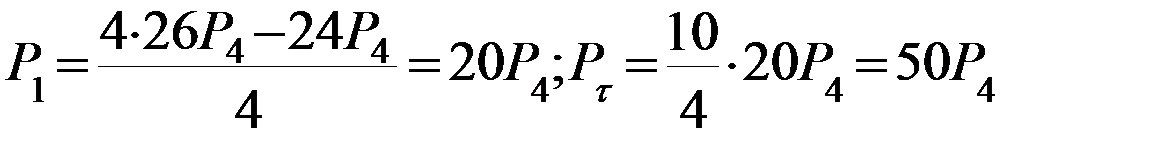
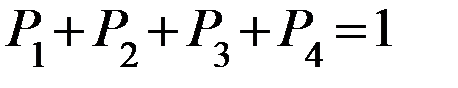
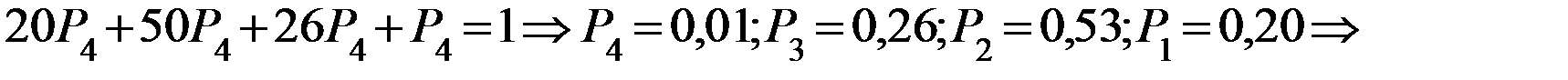 в установившемся режиме причал более половины времени (53%) будет простаивать из-за отсутствия судов с грузом, т.е. находится в состоянии
в установившемся режиме причал более половины времени (53%) будет простаивать из-за отсутствия судов с грузом, т.е. находится в состоянии 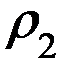 .
.
 46 % времени (Р1+Р3) у причала будет происходить выгрузка судов, причем большую часть времени выгрузка будет осуществляться 1 краном (
46 % времени (Р1+Р3) у причала будет происходить выгрузка судов, причем большую часть времени выгрузка будет осуществляться 1 краном ( 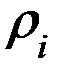 ) .
) .
В течении 1 % времени причал не сможет принимать суда из-за неисправности обоих кранов.
Зная эти величины, можно планировать объем перевозки грузов на причале и расходы.
Формула Эрланга
Поток Эрланга каждого порядка называется поток событий, полученный из исходного потока, в котором распределение вероятности продолжительности интервалов между событиями подчинена экспон. Закону, сохранением которых событий и отбрасывание поток Эрланга II порядка.
t1 t2 t3 t4 t
Вероятность появляется определенного числа событий, в потоке Эрланга подчинена Пуассоновскому закону. Т.к. в исходном потоке величина интервалов между событиями распределена по экспон. Закону, то и в Эрлангском потоке также распределена экспон-но.
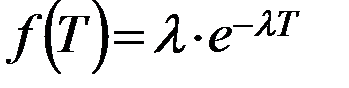
Если 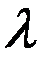 - плотность вероятности в исходном потоке.
- плотность вероятности в исходном потоке.
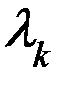 - плотность вероятности в Эрлангском потоке, которого порядко… соотношение между ними следующее:
- плотность вероятности в Эрлангском потоке, которого порядко… соотношение между ними следующее:
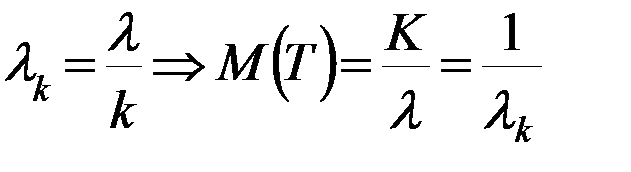
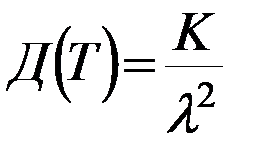 К- порядок потока Эрланга.
К- порядок потока Эрланга.
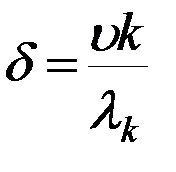
Понятие систем массового обслуживания (СМО). Их классификация.
Заявка- это требование на выполнение определенной однородной операции или это объект, требующий обслуживания.
Поток заявок приводит к тому, что с системой происходит поток событий.
СМО- это система, предназначенная для удовлетворения определенных однородных потребностей.
Поток заявок- это поток случайных событий, где случайными величинами являются число поступающих и обработанных заявок, моменты их поступления, продолжительность обслуживания и ожидания.
Для того чтобы СМО функционировала, она должна обладать каналами обслуживания – это люди или механизмы, которые осуществляют обслуживание.
Требования на обслуживание поступают на выполнение массовых операций  работа такой системы может быть представлена в виде потока случайных событий.
работа такой системы может быть представлена в виде потока случайных событий.
f.e. порт - СМО, судно - заявка, причал - канал.
Классификация СМО:
1). по числу каналов:
· одноканальные
· многоканальные
2). по характеру обслуживания:
· СМО с отказами
· СМО с ожиданием
СМО с отказами - заявка, поступающая, когда каналы обслуживания заняты, немедленно покидает систему.
СМО с ожиданиями –заявка, поступающая, когда каналы обслуживания заняты, встает в очередь в ожидании обслужи
Дата добавления: 2019-12-09; просмотров: 913;











