Нелинейного программирования.
1 y
x2 + y2 = 1
Z = f (x, y) 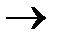 max -1 1 х
max -1 1 х
-1
Глобальный оптимум
Если область дополнительных значений (О. Д. З.) нелинейна и не выпукла, то появляется понятие локального оптимума и глобального оптимума.
Глобальный оптимум: здесь достигается оптимальное значение целевой функции по сравнению с любой другой точкой допустимого пространства.
В линейном программировании базисное и оптимальное решения содержат столько переменных, сколько ограничений имеется в данной задаче. Для нелинейного программирования данная закономерность не соблюдается.
Методы решения задач нелинейного
Программирования.
В отличие от линейного программирования одного универсального метода решение здесь не существует. Различаются 2 группы:
1) Детерминированные
2) Статические.
I. Детерминированные методы:
1) Градиентный (нормаль/перпендикуляр к касательной)
2) Метод наискорейшего спуска (подъёма)
3) Графический метод.
II. Статистические методы:
1) Метод Монте-Карло (случайных испытаний).
2) Метод случайного поиска.
3) Метод статистического градиента.
Рассмотрим пример использования графического метода из группы Ι.
Задача: необходимо спроектировать склад прямоугольной формы по критерию минимум строительных затрат.
| b=x a=y |

200у. руб.
Z = (780*x + 200*y)*2 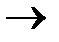 min
min
x > 0, y > 0
x 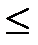 35(м) xy
35(м) xy  1000(м2)
1000(м2)
y
62,5
10 16 35 X
Тангенс угла наклона целевой функции = первой производной от нелинейного ограничения.
tg 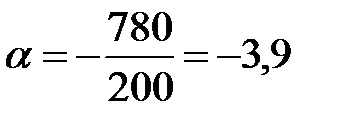
y’ = 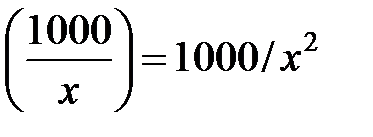
-3,9 = -1000 / х2
х = 16 у = 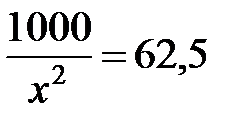
Дата добавления: 2019-12-09; просмотров: 896;











