Динамического программирования.

Динамическое программирование используется для решения многошаговых экономических и технических задач, т. е. решение находится не для определённого времени, а для многошагового растянутого во времени процесса.

Идея многошаговой оптимизации состоит в том, что оптимизируется каждый шаг в отдельности, но с учётом оптимизации на данном шаге на последующий шаг, т. е. используется системный подход. Т. к цель решения задачи достигается на конечном (последнем) шаге и единственным этапом, который не влияет на последующее является именно последний шаг, то обычно задача динамического программирования решается от последнего этапа к первому, т. е. в обратном направлении.

Для каждого возможного итога на предпоследнем шаге находится оптимальное решение на последнем шаге. Такой алгоритм называется условным оптимальным управлением.

Динамическое программирование основывается на принципе оптимальности Беллман:

«Если в процессе решения оптимизируется конкретный этап, то эта оптимизация является составной частью оптимизации процесса в целом (всякая часть оптимального пути оптимальна) ».

Преимущества пошагового решения.

Вместо решения сложной экономической задачи мы разбиваем её на несколько этапов и решаем поэтапно, увязывая при этом один этап с другими. При этом целевая функция может быть как линейной, так и нелинейной.

Недостаток:

Большой объём вычислений, отсутствие универсального метода решения. Задача должна чётко делится на этапы.

Одна из типичных задач динамического программирования – задача распределения ресурсов в любой отрасли экономики.

Пример:

Необходимо распределить ресурсы между объектами по годам с тем, чтобы за весь планируемый период эффективность использования планируемых ресурсов была бы максимальна.

Z₀ = исходное количество средств, которое надо распределить между объектами (предприятиями).

х – исходное количество средств, выделяемых 1-ому предприятию.

у – исходное количество средств, выделяемых 2-ому предприятию.

f (x)- заданная отдача (эффективность)

на каждый рубль вложенных средств в x.

g(x) - заданная отдача (эффективность)

на каждый рубль вложенных средств в y.

По условию оставшиеся к концу года средств снова распределяются между объектами. Цель: так распределить ресурсы по объектам и годам, чтобы за весь планируемый период получить max. объём доходов.

Разобьем каждый год (шаг) на 2 полушага.

1. Распределение средств на 1-ом году (или перераспределение на оставшихся годах)

2. Запланированные средства тратятся, происходит производственный процесс получение дохода.

Для i-ого года средств на начало года будет х_i – y_i , т. е. столько, сколько осталось от i – 1(предыдущего) года.

y

Z₀

C

Y_{1 1}

Д Е

Y₂ H

G

X₂ X

X₁ Z₀

Д (х₁, y₁) – средства, оставшиеся на конец первого года.

Е (х₂, y₂)

Путь СD – это производство в первом году (средства тратятся и извлекается доход)

Путь DЕ – перераспределение от оставшихся от первого года средств между двумя объектами.

ЕG – производство во втором году.

G ( 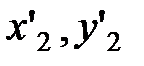) – осталось средств на конец второго года.

GH – перераспределение средств, оставшихся от второго года.

H ( 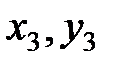) – распределение средств на конец второго года.

Вопросы, решаемые в ходе определения оптимального решения следующие:

1. с какой точки начать?

2. какой должна быть траектория движения?

Z =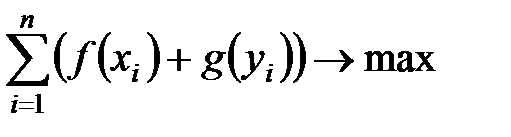

Данная задача имеет разновидности:

1) размер прибыльности меняется по годам.

2) Ресурсы должны быть распределены на большое количество лет.

3) Большое количество объектов.

4) Задачи с резервированием ресурсов, т. е. оставшиеся на конец года ресурсы не вкладываются в производство.

Задача:

- задача управления запасами.

- задача теории расписания (календарного планирования)