Одноканальные СМО с ограниченной очередью.

Число каналов n=1, емкость накопителя (max очередь) m=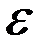

S0

S2

Sm+1

Sk

S1

…… ……

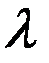
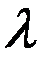
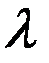
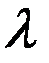
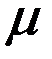
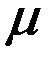
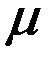
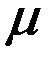
S₀ – канал свободный

S₁ – канал занят, очереди нет

S₂ - канал занят, в очереди 1 заявка

S_k – канал занят, в очереди К-1 заявка

S_m+1 – канал занят, в очереди m заявок (накопитель полностью заполнен)

Приравнивание уравнения Колмогорова-Чемпена к Ø и 3 состояния (S₂)

1). 1 состояние (S₀) получаем линейное уравнение:

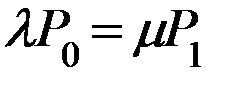
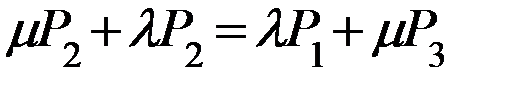
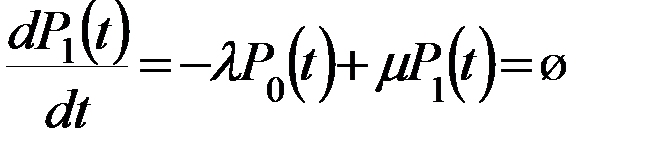
2 состояние (S₁)

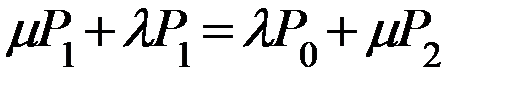
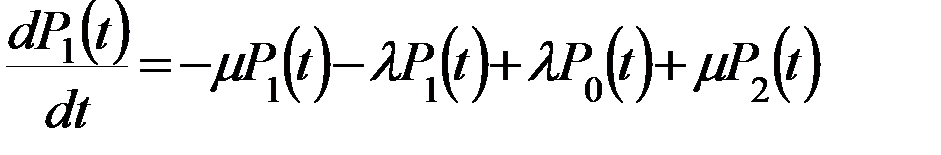
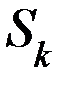
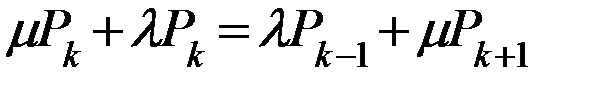
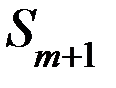
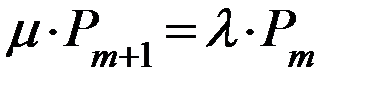
2). Преобразуем из уравнения, характерного Ø-ое состояние выражаем Р₁:

*

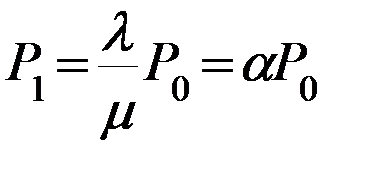
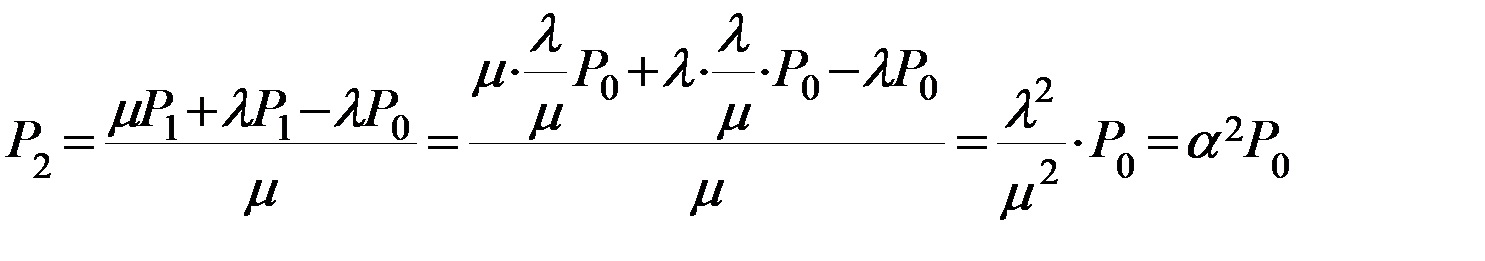
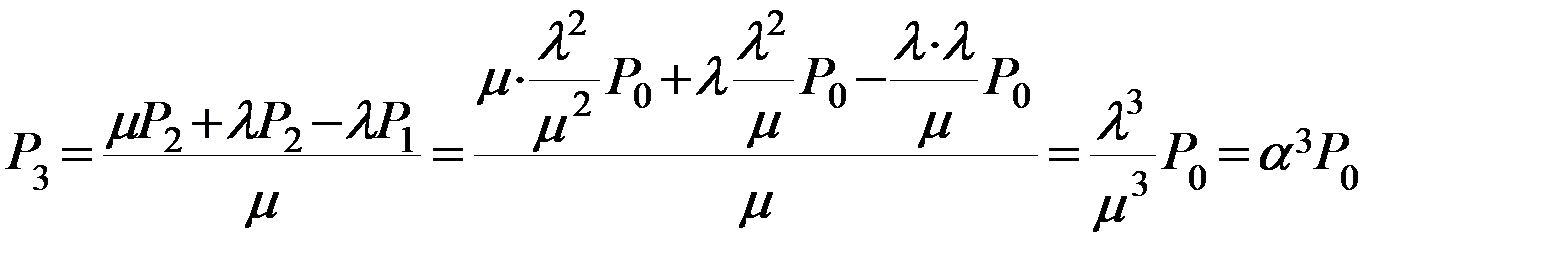
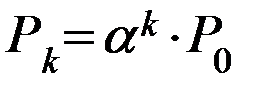
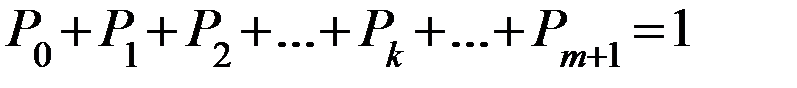
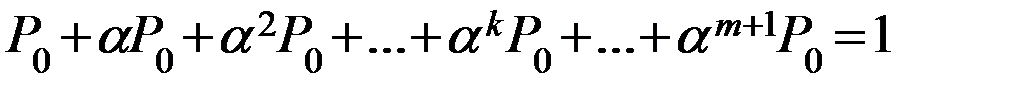
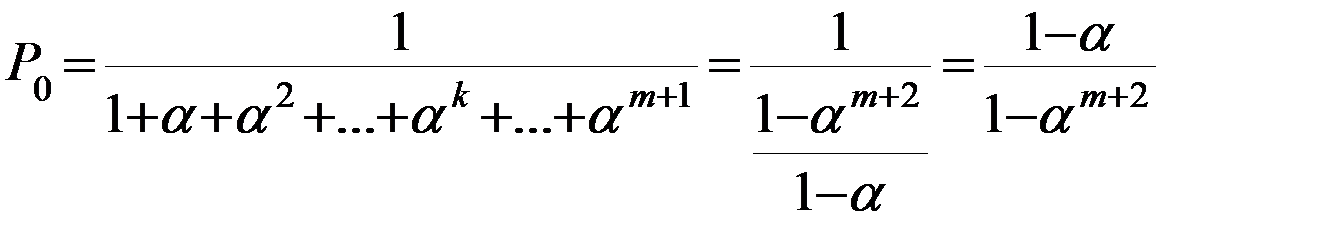
Геометрическая прогрессия

*

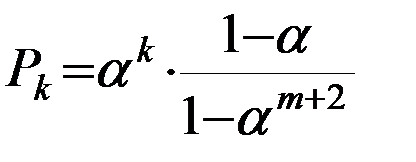
Последние системы уравнения (*) называются формулами Эрланга.

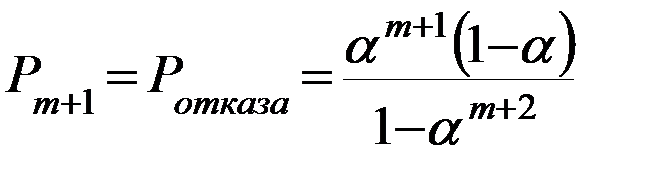
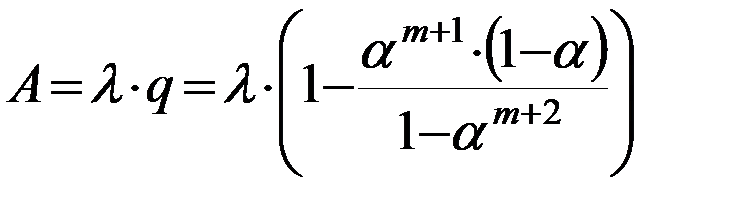
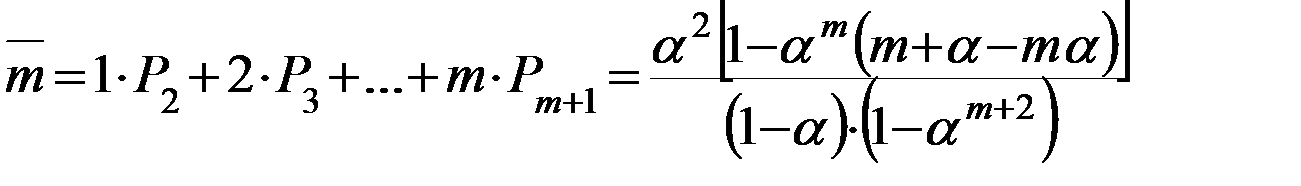
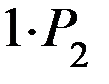- второе состояние

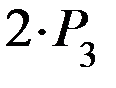- третье состояние

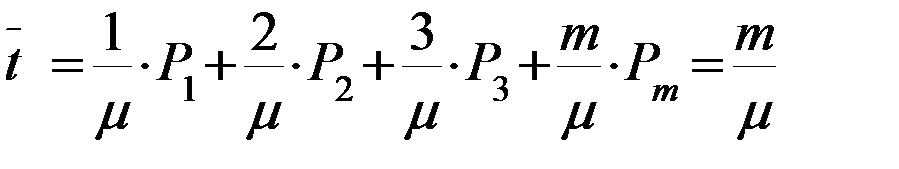
1, 2, ….., m – количество заявок.

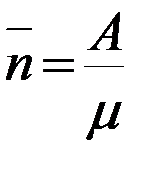
Величина относительного времени ожидания.

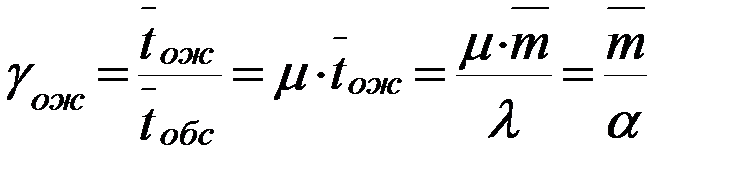
Пример: Пристань имеет 1 причал, входящий поток судов простейший, 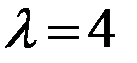, акватория ограничена 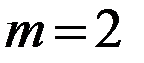. На пристань можно поставить следующее количество транспортеров 1, 2, 3. К=1 – то 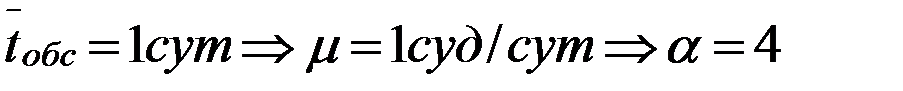. К-2 – то 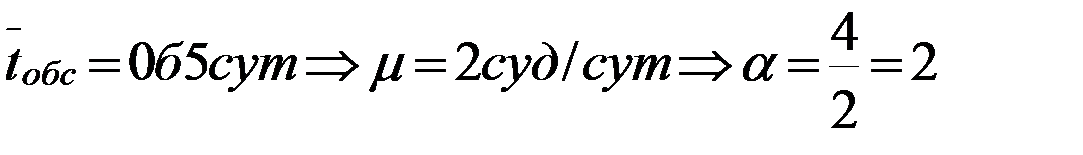. К-3 – то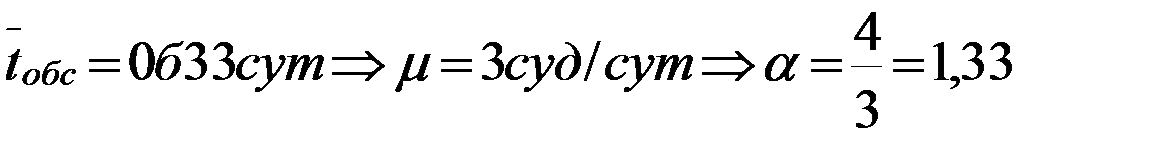

Рассчитать параметры системы для трех вариантов.

S₀ – состояние когда причал свободен, заявок нет

S₁ – канал занят, очереди нет

S₂ – канал занят, очередь 1 судно

S₃ – канал занят, очередь 2 судна

	К=1	К=2	К=3
Р0	0,01	0,07	0,16
Р1	0,04	0,14	0,21
Р2	0,16	0,28	0,28
Р3	0,79	0,51	0,38
q	0,21=Р0+Р1+Р2	0,49	0,62
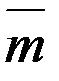
		1,3
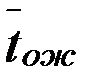
	0,5 сут	0,325 сут	0,25 сут

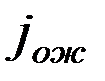
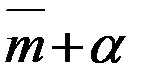
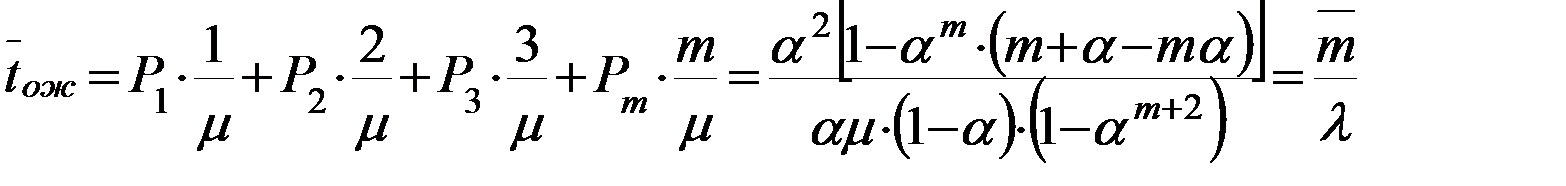
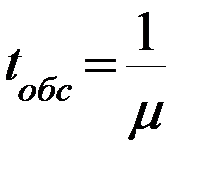
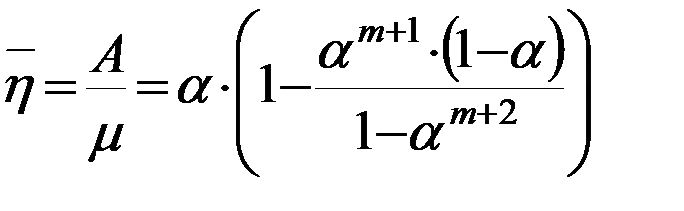
Среднее число занятых каналов обслуживания = среднему числу заявок, находящимся под обслуживанием.