Геометрическая вероятность.
Если опыт имеет бесконечное число исходов, то применять формулу классической вероятности нельзя.
Пример 6: На отрезок прямой [0; 5] наудачу ставится точка. Какова вероятность того, что она попадет в отрезок [1; 2]?
Отрезок [1; 2] включается в отрезок [0; 5]. Вероятность попадания точки на отрезок [1; 2] пропорциональна его длине и может быть найдена как отношение длин этих отрезков:
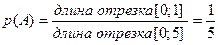 .
.
При обобщении этого результата используется понятие меры пространства n измерений. N-мерное пространство обозначим 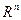 , произвольную область данного пространства -
, произвольную область данного пространства - 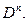 Считаем, что на
Считаем, что на 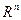 задана определенным образом мера области:
задана определенным образом мера области: 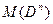 . Например, для
. Например, для 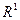 ,множества точек прямой, мера – длина отрезка, для
,множества точек прямой, мера – длина отрезка, для 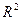 , множество точек плоскости, мера – площадь фигуры, для
, множество точек плоскости, мера – площадь фигуры, для 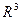 , множество точек пространства, мера– объем тела.
, множество точек пространства, мера– объем тела.
Пусть в области 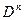 выделяется часть
выделяется часть 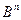 , и в области
, и в области 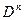 наудачу выбирается точка. Какова вероятность того, что эта точка попадет в область
наудачу выбирается точка. Какова вероятность того, что эта точка попадет в область 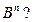
Если предположить, что попадание точки в область, пропорциональной только ее мере, получаем:
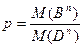
Данную формулу называют формулой геометрической вероятности.
Использование геометрической вероятности обосновано тогда, когда пространство элементарных событий бесконечно и может быть описано с помощью геометрических величин.
Пример 7. Из отрезка [0, 1] наудачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам х > 2у.
Решение. Выбор пары чисел можно интерпретировать как выбор точки на плоскости. По условиям опыта координаты точки (х, у) удовлетворяют системе неравенств 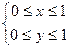 .
.
Это значит, что точка (х, у) наудачу выбирается из множества точек единичного квадрата, пространство элементарных событий бесконечно и геометрически представлено множеством точек квадрата. Элементарные события, при которых наступает событие А- « х > у» соответствуют точкам заштрихованного треугольника (рис.1 ).
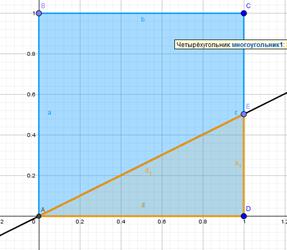
Рис.1.
Следовательно, искомая вероятность равна отношению площади заштрихованного треугольника ( 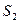 ) к площади квадрата (
) к площади квадрата ( 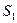 ):
): 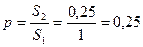
Дата добавления: 2018-11-26; просмотров: 1023;











