Геометрическая вероятность.
В одном специальном случае дадим правило расчёта вероятности события для случайного эксперимента с несчетным множеством исходов.
Если между множествомW элементарных исходов случайного эксперимента и множеством точек некоторой плоской фигуры S (сигма большая) можно установить взаимно-однозначное соответствие, а также можно установить взаимно-однозначное соответствие между множеством элементарных исходов, благоприятствующих событию А, и множеством точек плоской фигуры s (сигма малая), являющейся частью фигуры S, то
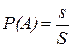 ,
,
где s — площадь фигуры s, S — площадь фигуры S. Здесь, естественно, подразумевается, что фигуры S и s имеют площади. Например, фигура s может представлять собой отрезок прямой линии с площадью, равной нулю.
Заметим, что в этом определении вместо плоской фигуры S можно рассматривать промежуток S, а вместо её части s — промежуток s, целиком принадлежащий промежутку s, и вероятность представлять как отношение длин соответствующих промежутков.
Пример 3. Два человека обедают в столовой, которая открыта с 12 до 13 часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какова вероятность их встречи?
Пусть x — время прихода первого в столовую, а y — время прихода второго. Тогда 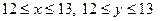 .
.
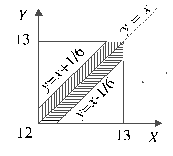
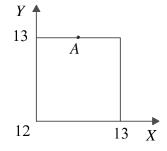 Можно установить взаимно-однозначное соответствие между всеми парами чисел (x;y) (или множеством исходов) и множеством точек квадрата со стороной, равной 1, на координатной плоскости, где начало координат соответствует числу 12 по оси X и по оси Y, как изображено на рисунке. Здесь, например, точка А соответствует исходу, заключающемуся в том, что первый пришел в 12.30, а второй — в 13.00. В этом случае, очевидно, встреча не состоялась.
Можно установить взаимно-однозначное соответствие между всеми парами чисел (x;y) (или множеством исходов) и множеством точек квадрата со стороной, равной 1, на координатной плоскости, где начало координат соответствует числу 12 по оси X и по оси Y, как изображено на рисунке. Здесь, например, точка А соответствует исходу, заключающемуся в том, что первый пришел в 12.30, а второй — в 13.00. В этом случае, очевидно, встреча не состоялась.
Если первый пришел не позже второго (y ³ x), то встреча произойдет при условии 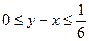 , т.к. 10 минут — это 1/6 часа.
, т.к. 10 минут — это 1/6 часа.
|
Если второй пришел не позже первого (x ³ y), то встреча произойдет при условии 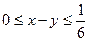 .
.
Между множеством исходов, благоприятствующих встрече, и множеством точек области s, изображенной на рисунке в заштрихованном виде, можно установить взаимно-однозначное соответствие.
Искомая вероятность p равна отношению площади области s к площади всего квадрата. Площадь квадрата равна единице, а площадь области s можно определить как разность единицы и суммарной площади двух треугольников. Отсюда следует:
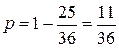 .
.
Дата добавления: 2021-11-16; просмотров: 688;











